题目内容
在平面直角坐标系xOy中,直线l的参数方程为
(t为参数),曲线C的参数方程为
(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
|
|
考点:参数方程化成普通方程
专题:直线与圆
分析:把直线和曲线的参数方程用代入法消去参数化为普通方程,联立方程组求得两个曲线的交点的坐标.
解答:
解:∵直线l的参数方程为
(t为参数),∴y=2(x-1),即 2x-y-2=0.
由曲线C的参数方程为
(θ为参数),可得 x=2(
)2,即 y2=2x.
由
求得
,或
,
故它们的公共点的坐标为(
,-1)、(2,2).
|
由曲线C的参数方程为
|
| y |
| 2 |
由
|
|
|
故它们的公共点的坐标为(
| 1 |
| 2 |
点评:本题主要考查把参数方程化为普通方程的方法,求两个曲线的交点坐标,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
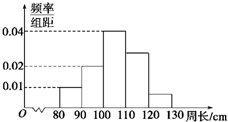 为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )
为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )| A、3000 | B、6000 |
| C、7000 | D、8000 |
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )| A、a=b=c |
| B、a<c<b |
| C、a<b<c |
| D、b<a<c |
 如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.
如图所示的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=2AB,CE与平面ACD所成角为45°,F、H分别为CD、DE中点.