题目内容
函数f(x)=
的值域是( )
|
| A、(0,+∞) | ||
| B、(0,1) | ||
C、[
| ||
D、[
|
考点:函数的值域
专题:函数的性质及应用
分析:本题考查的是分段函数的值域,分别运用了二次函数和幂函数(反比例函数)的单调性.
解答:
解:当x<1时,f(x)=(x-
)2+
,在(-∞,
)上单调递减,在(
,1)上单调递增,所以f(x)≥
,
当x>1时,f(x)=
,单调递减,所以f(x)∈(0,1),综合以上得函数f(x)的值域数(0,+∞).
故答案为A.
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
当x>1时,f(x)=
| 1 |
| x |
故答案为A.
点评:二次函数的单调性是由对称轴的确定的,反比例函数的单调性是由比例系数k的正负性来定的,分段函数的值域是各段的值域的并集.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
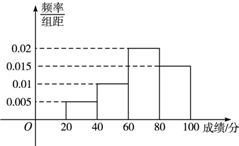 某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],则该次英语测试该班的平均成绩是( )| A、63 | B、65 | C、68 | D、70 |
已知全集U={0,1,2,3,4},集合A={1,2},B={2,3,4},则B∩∁UA的子集个数有( )
| A、2 | B、4 | C、8 | D、16 |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
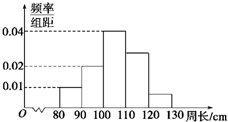 为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )
为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )| A、3000 | B、6000 |
| C、7000 | D、8000 |
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十进制)如图所示,假设得分值的中位数为a,众数为b,平均值为c,则( )| A、a=b=c |
| B、a<c<b |
| C、a<b<c |
| D、b<a<c |