题目内容
在0、1、2、3、5中任取4个数组成没重复的四位数,且使该四位数能被剩下的数除尽,这样的数共有 .
考点:计数原理的应用,排列、组合的实际应用
专题:应用题,排列组合
分析:分类讨论,考虑剩0,1,2,3,5,分别求得相应数的个数,即可得出结论.
解答:
解:剩0,舍去
剩1,都可除尽,有3×3×2×1=18个
剩2,末位为0可除尽,有3×2×1×1=6个
剩3,0+1+2+5=8,不可除尽
剩5,末位为0可除尽,有3×2×1×1=6个,
故共有18+6+6=30个.
故答案为:30个.
剩1,都可除尽,有3×3×2×1=18个
剩2,末位为0可除尽,有3×2×1×1=6个
剩3,0+1+2+5=8,不可除尽
剩5,末位为0可除尽,有3×2×1×1=6个,
故共有18+6+6=30个.
故答案为:30个.
点评:本题考查计数原理的运用,考查分类讨论的数学思想,考查学生的计算能力,属于基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
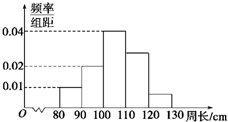 为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )
为了解一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出的样本频率分布直方图如图所示,那么在这片树木中,底部周长小于110cm的株数大约是( )| A、3000 | B、6000 |
| C、7000 | D、8000 |
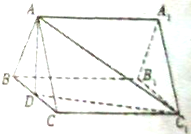 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为2,且侧棱AA1⊥底面ABC,点D是BC的中点
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的正三角形,侧棱长为2,且侧棱AA1⊥底面ABC,点D是BC的中点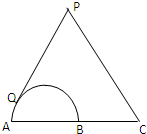 如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若
如图,点C为半圆的直径AB延长线上一点,AB=BC=2,过动点P作半圆的切线PQ,若