题目内容
在数列{an}中,a2n=qn,a2n-1=d(n+1),(n∈N*),且前n项和为Sn,若a5=S2=8.
(1)求实数q,d;
(2)求数列{an}的前n项和为Sn.
(1)求实数q,d;
(2)求数列{an}的前n项和为Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件列出方程组,能求出实数q,d.
(2)由(1)知an=
,由此按n为偶数和n为奇数两种情况进行分类讨论,能求出数列{an}的前n项和为Sn.
(2)由(1)知an=
|
解答:
解:(1)在数列{an}中,
∵a2n=qn,a2n-1=d(n+1),(n∈N*),a5=S2=8.
∴
,
解得d=2,q=4.
(2)由(1)知a2n=4n,a2n-1=2(n+1),
∴an=
,
①当n为偶数时,前n项和:
Sn=[4+6+8+…+(n-1+3)]+(22+24+…+2n)=
+
.
②当n为奇数时,前n项和:
Sn=[4+6+8+…+(n+3)]+(22+24+…+2n-1)=
+
.
∵a2n=qn,a2n-1=d(n+1),(n∈N*),a5=S2=8.
∴
|
解得d=2,q=4.
(2)由(1)知a2n=4n,a2n-1=2(n+1),
∴an=
|
①当n为偶数时,前n项和:
Sn=[4+6+8+…+(n-1+3)]+(22+24+…+2n)=
| n2+6n |
| 4 |
| 2n+2-4 |
| 3 |
②当n为奇数时,前n项和:
Sn=[4+6+8+…+(n+3)]+(22+24+…+2n-1)=
| n2+8n+7 |
| 4 |
| 2n+1-4 |
| 3 |
点评:本题考查数列中参数的求法,考查数列的前n项和的求法,是中档题,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )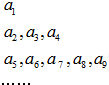 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.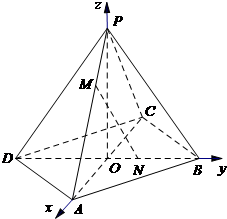 如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为
如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为