已知2f=3x+2.求函数f(x)的解析式．题目和参考答案——青夏教育精英家教网—

题目内容

已知2f（x）+f（-x）=3x+2，求函数f（x）的解析式．

考点：函数解析式的求解及常用方法

专题：函数的性质及应用

分析：由题意，2f（x）+f（-x）=3x+2为①式，以-x代替x，得②式；由①②组成方程组，求出f（x）即可．

解答： 解：∵2f（x）+f（-x）=3x+2，①；
令x=-x，得2f（-x）+f（x）=-3x+2，②；
再由①×2-②，得：
3f（x）=9x+2；
∴f（x）=3x+

．

点评：本题考查的知识点是函数解析式的求解方法--方程组法，熟练掌握方程组法求解析式的适用范围和步骤是解答的关键．

练习册系列答案

相关题目

，则目标函数z=2x-3y的最大值（　　）

）．
（1）求f（x）的最小值，并求使f（x）取得最小值的x的集合；
（2）在△ABC中，设角A，B的对边分别为a，b，若B=2A，且b=2af（A-

），求角C的大小．

已知函数f（x）=x⁴+x²-1，g（x）=ax³+x²+b（x∈R），其中a，b∈R．
（Ⅰ）若曲线y=f（x）与y=g（x）在点（1，1）处相交且有相同的切线，求a，b的值；
（Ⅱ）设F（x）=f（x）+g（x），若对于任意的a∈[-2，2]，函数y=F（x）在区间[-1，1]上的值恒为负数，求b的取值范围．

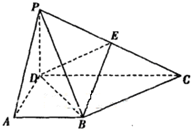在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，底面ABCD是直角梯形，AB∥DC，∠ADC=90°，AB=AD=PD=1，CD=2．
（Ⅰ）求证：BC⊥平面PBD：
（Ⅱ）求直线AP与平面PDB所成角的正弦值；
（Ⅲ）设E为侧棱PC上异于端点的一点，

=λ

，试确定λ的值，使得二面角E-BD-P的余弦值为

．

在数列{a_n}中，a2n=qn，a2n-1=d(n+1)，(n∈N*)，且前n项和为S_n，若a₅=S₂=8．
（1）求实数q，d；
（2）求数列{a_n}的前n项和为S_n．

已知函数f(x)=

+lnx-1，g（x）=（lnx-1）e^x+x（其中e为自然对数的底数）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）是否存在实数x₀∈（0，+∞），使曲线y=g（x）在点x=x₀处的切线与y轴垂直？若存在，求出x₀的值；若不存在，请说明理由；
（Ⅲ）若实数m，n满足m＞0，n＞0，求证：nⁿe^m≥mⁿeⁿ．

已知扇形的周长为定值l，写出扇形的面积y关于其半径x的函数解析式

．

试题分类