题目内容

1．已知集合A={x|y=lg（x+1）}，B={x||x|＜2}，则A∩B=（　　）
A．（-2，0）B．（0，2）C．（-1，2）D．（-2，-1）

分析 求解对数型函数的定义域化简集合A，然后直接利用交集运算求解．

解答 解：由x+1＞0，得x＞-1
∴A=（-1，+∞），
B={x||x|＜2}=（-2，2）
∴A∩B=（-1，2）．
故选：C

点评 本题考查了交集及其运算，考查了对数函数的定义域，是基础题．

练习册系列答案
相关题目
17．某同学在高三学年的五次阶段性考试中，数学成绩依次为110，114，121，119，126，则这组数据的方差是
30.8．
12．设集合A={x|（x+1）（4-x）＞0}，B={x|0＜x＜9}，则A∩B等于（　　）
A．（0，4）B．（4，9）C．（-1，4）D．（-1，9）
9．已知函数f（x）=|x-2|-4，g（x）=|x+1|-3．
（Ⅰ）若f（x）≤1，求实数x的取值范围；
（Ⅱ）若不等式f（x）-g（x）≥m-1有解，求实数m的取值范围．
16．已知函数f（x）=m-|x-3|，若不等式f（x）＞2的解集为（2，4），则实数m的值为3．
6．已知双曲线经过点$（{1，2\sqrt{2}}）$，其一条渐近线方程为y=2x，则该双曲线的标准方程为$\frac{{y}^{2}}{4}$-x2=1．
13．已知向量$\overrightarrow m=（\sqrt{3}sin\frac{x}{4}，1），\overrightarrow n=（cos\frac{x}{4}，cos_{\;}^2\frac{x}{4}）．记f（x）=\overrightarrow m•\overrightarrow n$．
（1）若f（α）=$\frac{3}{2}，求cos（\frac{2π}{3}-α）$的值；
（2）在△ABC中，角A、B、C的对边分别是a、b、c，且满足（2a-c）cos B=bcos C，若f（A）=$\frac{{1+\sqrt{3}}}{2}$，试判断△ABC的形状．
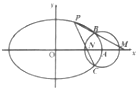10．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的长轴长为4，焦距为$2\sqrt{3}$，以A为圆心的圆（x-2）2+y2=r2（r＞0）与椭圆相交于B、C两点．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）求$\overrightarrow{AB}•\overrightarrow{AC}$的取值范围；
（Ⅲ）设P是椭圆C长异于B、C的任一点，直线PB、PC与x轴分别交于M、N，
求S△POM•S△PON的最大值．
11．某人欲投资A，B两支股票时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损，根据预测，A，B两支股票可能的最大盈利率分别为40%和80%，可能的最大亏损率分别为10%和30%．若投资金额不超过15万元．根据投资意向，A股的投资额不大于B股投资额的3倍，且确保可能的资金亏损不超过2.7万元，设该人分别用x万元，y万元投资A，B两支股票．
（Ⅰ）用x，y列出满足投资条件的数学关系式，并画出相应的平面区域；
（Ⅱ）问该人对A，B两支股票各投资多少万元，才能使可能的盈利最大？并求出此最大利润．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网