题目内容
6.已知双曲线经过点$({1,2\sqrt{2}})$,其一条渐近线方程为y=2x,则该双曲线的标准方程为$\frac{{y}^{2}}{4}$-x2=1.分析 根据题意,由双曲线的渐近线方程,可以设其方程为x2-$\frac{{y}^{2}}{4}$=m,又由其过点$({1,2\sqrt{2}})$,将点的坐标代入方程计算可得m的值,即可得其方程,最后将求得的方程化为标准方程即可得答案.
解答 解:根据题意,双曲线的一条渐近线方程为y=2x,则可以设其方程为x2-$\frac{{y}^{2}}{4}$=m,(m≠0),
又由其经过点$({1,2\sqrt{2}})$,则有1-$\frac{(2\sqrt{2})^{2}}{4}$=m,
解可得m=-1,
则其方程为:x2-$\frac{{y}^{2}}{4}$=-1,
其标准方程为:$\frac{{y}^{2}}{4}$-x2=1,
故答案为:$\frac{{y}^{2}}{4}$-x2=1.
点评 本题考查双曲线的几何性质,注意最后的答案要检验其是否为标准方程的形式.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
1.已知集合A={x|y=lg(x+1)},B={x||x|<2},则A∩B=( )
| A. | (-2,0) | B. | (0,2) | C. | (-1,2) | D. | (-2,-1) |
11.已知函数f(x)=$\left\{\begin{array}{l}{3x+3(x≤-1)}\\{f(x-1)+1(x>-1)}\end{array}\right.$,方程f(x)=x+1的解从小到大排成一个数列{an},该数列的前n项和为Sn,则$\frac{2{S}_{n+3}+10}{n}$的最小值为( )
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
18.已知集合U={1,2,3,4,5,6},集合A={2,3},集合B={1,2,4},则(∁UB)∩A=( )
| A. | {2} | B. | {3} | C. | {5,6} | D. | {3,5,6} |
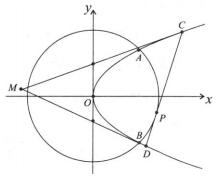 如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.
如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.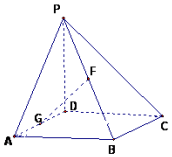 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,G,F分别是AD,PB的中点.