题目内容
设z=
+i,则|z|= .
| 1 |
| 1+i |
考点:复数求模
专题:数系的扩充和复数
分析:直接利用是分母实数化,然后求模即可.
解答:
解:z=
+i=
+i=
+
i.
|z|=
=
.
故答案为:
.
| 1 |
| 1+i |
| 1-i |
| (1+i)(1-i) |
| 1 |
| 2 |
| 1 |
| 2 |
|z|=
(
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查复数的代数形式的混合运算,复数的模的求法,考查计算能力.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
已知△ABC的内角A,B,C对应的边分别为a,b,c,且
=
,则△ABC为( )
| c |
| a |
| cosB |
| 1+cosA |
| A、等边三角形 |
| B、等腰直角三角形 |
| C、直角三角形 |
| D、三边均不相等的三角形 |
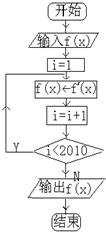
程序框图如图所示,该程序运行后输出的S的值是( )


A、
| ||
| B、-3 | ||
C、-
| ||
| D、2 |
设全集为实数集R,M={x|x2>4},N={x|1<x≤3},则图中阴影部分表示的集合是( ) 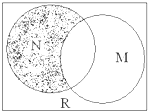

| A、{x|1-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|x<2} |
设集合A={x|x2-5x+4<0},B={y|-1<y<3},则A∩(∁RB)=( )
| A、(1,4) |
| B、[3,4) |
| C、(1,3) |
| D、(1,2)∪(3,4) |
集合A={x|y=ln(-x2+2x+3)},B={y|y=ex},则A∩B=( )
| A、{x|-1<x<0} |
| B、{x|0<x<3} |
| C、{x|x>-1} |
| D、{x|x<3} |