题目内容
若函数f(x)=sinax(a>0)的最小正周期为12,求f(1)+f(2)+f(3)+…f(2012).
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:由函数的周期为12求得a的值,可得函数的解析式,再利用函数的周期性,求所给式子的值.
解答:
解:由题意可得,f(x)的最小正周期为
=12,∴a=
,f(x)=sin
x.
由于f(1)+f(2)+f(3)+…f(12)=0,2012=12×167+8,
∴f(1)+f(2)+f(3)+…f(2012)=167×0+f(1)+f(2)+f(3)+…f(8)=
.
| 2π |
| a |
| π |
| 6 |
| π |
| 6 |
由于f(1)+f(2)+f(3)+…f(12)=0,2012=12×167+8,
∴f(1)+f(2)+f(3)+…f(2012)=167×0+f(1)+f(2)+f(3)+…f(8)=
3+
| ||
| 2 |
点评:本题主要考查正弦函数的周期性,利用函数的周期性,求函数的值,属于基础题.

练习册系列答案
相关题目
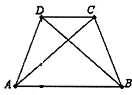 在等腰梯形ABCD中,AB∥CD,且AB>CD.设以A,B为焦点且过点D的双曲线的离心率为2,以C,D为焦点且过点A的椭圆的离心率e等于( )
在等腰梯形ABCD中,AB∥CD,且AB>CD.设以A,B为焦点且过点D的双曲线的离心率为2,以C,D为焦点且过点A的椭圆的离心率e等于( )