题目内容
11.已知二次函数f(x)=ax2+bx+c(a,b,c∈R),对任意实数x,不等式$2x≤f(x)≤\frac{1}{2}{(x+1)^2}$恒成立,(Ⅰ)求f(-1)的取值范围;
(Ⅱ)对任意x1,x2∈[-3,-1],恒有|f(x1)-f(x2)|≤1,求实数a的取值范围.
分析 (Ⅰ))根据不等式,先令x=1,可得f(1)=2,即a+b+c=2,再由不等式恒成立,结合二次函数的判别式小于等于0,及配方思想,可得a的范围,进而得到f(-1)=4a-2,可得范围.
(2)对任意x1,x2∈[-3,-1],恒有|f(x1)-f(x2)|≤1,f(x)max-f(x)min≤1,结合二次函数的图象和性质分类讨论,可得实数a的取值范围.
解答 解:(Ⅰ) 由题意可知f(1)≥2,f(1)≤2,
∴f(1)=2,
∴a+b+c=2,
∵对任意实数x都有f(x)≥2x,即ax2+(b-2)x+c≥0恒成立,
∴$\left\{\begin{array}{l}a>0\\{(b-2)^2}-4ac≤0\end{array}\right.$,由a+b+c=2,
∴a=c,b=2-2a,
此时$f(x)-\frac{1}{2}{(x+1)^2}=(a-\frac{1}{2}){(x-1)^2}$,
∵对任意实数x都有$f(x)≤\frac{1}{2}{(x+1)^2}$成立,
∴$0<a≤\frac{1}{2}$,
∴f(-1)=a-b+c=4a-2的取值范围是(-2,0].
(Ⅱ) 对任意x1,x2∈[-3,-1]都有|f(x1)-f(x2)|≤1等价于在[-3,-1]上的最大值与最小值之差M≤1,
由(1)知 $f(x)=a{x^2}+2(1-a)x+a,a∈(0,\frac{1}{2}]$,
即$f(x)=a{(x-\frac{a-1}{a})^2}+2-\frac{1}{a}$,对称轴:${x_0}=1-\frac{1}{a}∈(-∞,-1]$,
据此分类讨论如下:
(ⅰ)当-2<x0≤-1即$\frac{1}{3}<a≤\frac{1}{2}$时,$M=f(-3)-f({x_0})=16a+\frac{1}{a}-8≤1$,$⇒\frac{{9-\sqrt{17}}}{32}≤a≤\frac{{9+\sqrt{17}}}{32}$$⇒\frac{1}{3}<a≤\frac{{9+\sqrt{17}}}{32}$.
(ⅱ) 当-3<x0≤-2,即$\frac{1}{4}<a≤\frac{1}{3}$时,$M=f(-1)-f({x_0})=4a+\frac{1}{a}-4≤1$恒成立.
(ⅲ)当x0≤-3,即$0<a≤\frac{1}{4}$时,M=f(-1)-f(-3)=4-12a≤1$⇒a=\frac{1}{4}$.
综上可知,$\frac{1}{4}≤a≤\frac{{9+\sqrt{17}}}{32}$.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.综合较强,有一定的难度.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案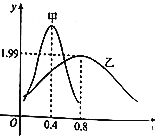 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )| A. | 乙类水果的质量服从的正态分布的参数σ2=1.99 | |
| B. | 甲类水果的质量比乙类水果的质量更集中 | |
| C. | 甲类水果的平均质量μ1=0.4kg | |
| D. | 甲类水果的平均质量比乙类水果的平均质量小 |
| A. | {x|x=2kπ+$\frac{4π}{3}$,k∈Z} | B. | {x|x=2kπ+$\frac{π}{3}$,k∈Z} | C. | {$\frac{4π}{3}$,$\frac{π}{3}$} | D. | {x|x=kπ+$\frac{π}{3}$,k∈Z} |
 阅读右面的程序框图,当该程序运行后输出的x的值是13.
阅读右面的程序框图,当该程序运行后输出的x的值是13.