题目内容
2.已知函数f(x)是定义在R上的奇函数,当x>0时,$f(x)=\frac{1}{2}({|{x-1}|+|{x-2}|-3})$.(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若对任意的x∈R,恒有f(x)≤f(x+a),求正实数a的取值范围.
分析 (1)利用函数f(x)是定义在R上的奇函数,且当x>0时,$f(x)=\frac{1}{2}({|{x-1}|+|{x-2}|-3})$,可求得当x<0时f(x)=-$\frac{1}{2}(|x+1|+|x+2|-3)$,从而可得f(x)的解析式;
(2)由f(x)=$\frac{1}{2}(|x-1|+|x-2|-3)$=$\left\{\begin{array}{l}{x+3,x<-2}\\{1,-2≤x≤-1}\\{-x,-1<x<1}\\{-1,1≤x≤2}\\{x-3,x>2}\end{array}\right.$即可画出f(x)的图象;
(3)依题意,可得f(x+a)的图象恒在f(x)的图象上方或部分重合,所以只需函数y=f(x+a)的图象与x轴最右边的交点P(-a+3,0)在函数y=f(x)的图象与x轴最左边的交点(-3,0)的左侧或与点(-3,0)重合即可求得正实数a的取值范围.
解答 解:(1)∵函数f(x)是定义在R上的奇函数,
当x>0时,$f(x)=\frac{1}{2}({|{x-1}|+|{x-2}|-3})$.
∴当x<0时,-x>0,f(-x)=$\frac{1}{2}(|-x-1|+|-x-2|-3)$=-f(x),
∴f(x)=-$\frac{1}{2}(|x+1|+|x+2|-3)$,
∴f(x)=$\frac{1}{2}(|x-1|+|x-2|-3)$=$\left\{\begin{array}{l}{x+3,x<-2}\\{1,-2≤x≤-1}\\{-x,-1<x<1}\\{-1,1≤x≤2}\\{x-3,x>2}\end{array}\right.$;
(2)画出f(x)的图象如下: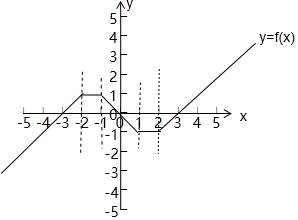
(3)∵a>0,
∴函数y=f(x+a)的图象是函数y=f(x)的图象向左平移a个单位得到的,
又对任意的x∈R,恒有f(x)≤f(x+a),
∴只需f(x+a)的图象恒在f(x)的图象上方或部分重合,
所以只需函数y=f(x+a)的图象与x轴最右边的交点P(-a+3,0)在函数y=f(x)的图象与x轴最左边的交点(-3,0)的左侧或与点(-3,0)重合,
∴-a+3≤-3,
∴a≥6.
点评 本题考查抽象函数及其应用,考查利用函数的奇偶性确定函数解析式及作图能力,对于(3)分析出y=f(x+a)与x轴最右边的交点在y=f(x)与x轴最左边交点的左边或重合是关键,也是难点,考查推理与运算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | $2\sqrt{3}$ | B. | $2\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | $\sqrt{13}$ |
 传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
| 优秀 | 合格 | 合计 | |
| 大学组 | |||
| 中学组 | |||
| 合计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.005 |
| k0 | 2.706 | 3.841 | 7.879 |
(Ⅲ)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6,在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为a,在选出的6名良好等级的选手中任取一名,记其编号为b,求使得方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$有唯一一组实数解(x,y)的概率.
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |