题目内容
已知p:实数x满足x2-4ax+3a2<0,其中a>0; q:实数x满足2<x≤3.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:(1)先通过解一元二次不等式求出p下的x的取值范围:a<x<3a,a=1时,所以p:1<x<3.根据p∧q为真得p,q都真,所以
,所以解该不等式组即得x的取值范围;
(2)若p是q的必要不充分条件,则:
,所以解该不等式组即得a的取值范围.
|
(2)若p是q的必要不充分条件,则:
|
解答:
解:(1)p:由原不等式得,(x-3a)(x-a)<0,∵a>0为,所以a<x<3a;
当a=1时,得到1<x<3;
q:实数x满足2<x≤3;
若p∧q为真,则p真且q真,∴实数x的取值范围是:(2,3);
(2)p是q的必要不充分条件,即由p得不到q,而由q能得到p;
∴
,解得1<a≤2;
∴实数a的取值范围是(1,2].
当a=1时,得到1<x<3;
q:实数x满足2<x≤3;
若p∧q为真,则p真且q真,∴实数x的取值范围是:(2,3);
(2)p是q的必要不充分条件,即由p得不到q,而由q能得到p;
∴
|
∴实数a的取值范围是(1,2].
点评:考查解一元二次不等式,p∧q的真假和p,q真假的关系,以及充分条件、必要条件、必要不充分条件的概念.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
在△ABC中,若三个内角A,B,C成等差数列且A<B<C,则cosAcosC的取值范围是( )
A、(-
| ||||
B、[-
| ||||
C、(-
| ||||
D、(-
|
已知函数f(x)=sin2x+2
cos2x-
,函数g(x)=mcos(2x-
)-2m+3(m>0),若?x1∈[0,
],总?x2∈[0,
],使得g(x1)=f(x2)成立,则实数m的取值范围为( )
| 3 |
| 3 |
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| A、[1,2] | ||||
B、[1,
| ||||
C、[
| ||||
D、[
|
不等式组
表示的平面区域面积是( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知集合A={x|x2-x-2≤0},B={x|y=ln(1-x)},则A∩B=( )
| A、(1,2) |
| B、(1,2] |
| C、[-1,1) |
| D、(-1,1) |
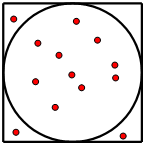 某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为35粒,则由此估计出的圆周率π的值为
某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为35粒,则由此估计出的圆周率π的值为