题目内容
已知函数f(x)=ax-
(a,b∈N*),f(1)=
且f(2)<2.
(Ⅰ)求a,b的值;
(Ⅱ)判断并证明函数y=f(x)在区间(-1,+∞)上的单调性.
| b |
| x+1 |
| 1 |
| 2 |
(Ⅰ)求a,b的值;
(Ⅱ)判断并证明函数y=f(x)在区间(-1,+∞)上的单调性.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由 f(1)=a-
=
,a=
,f(2)=2a-
<2,从而求出b=1,a=1;
(Ⅱ)由(1)得f(x)=x-
,得函数在(-1,+∞)单调递增.从而有f(x1 )-f(x2 )=(x1-x2)+
=(x1-x2)[1+
],进而(x1-x2)[1+
]<0,故函数f(x)=x-
在(-1,+∞)上单调递增.
| b |
| 2 |
| 1 |
| 2 |
| b+1 |
| 2 |
| b |
| 3 |
(Ⅱ)由(1)得f(x)=x-
| 1 |
| x+1 |
| x1-x2 |
| (x1+1)(x2+1) |
| 1 |
| (x1+1)(x2+1) |
| 1 |
| (x1+1)(x2+1) |
| 1 |
| x+1 |
解答:
解:(Ⅰ)∵f(1)=a-
=
,a=
,
由f(2)=2a-
<2,
∴b<
,
又∵a,b∈N*,
∴b=1,a=1;
(Ⅱ)由(1)得f(x)=x-
,
函数在(-1,+∞)单调递增.
证明:任取x1,x2且-1<x1<x2,
f(x1)-f(x2)=x1-
-(x2-
)=(x1-x2)+(
-
)
=(x1-x2)+
=(x1-x2)[1+
],
∵-1<x1<x2,
∴x1-x2<0,1+
>0,
∴(x1-x2)[1+
]<0,
即f(x1)<f(x2),
故函数f(x)=x-
在(-1,+∞)上单调递增.
| b |
| 2 |
| 1 |
| 2 |
| b+1 |
| 2 |
由f(2)=2a-
| b |
| 3 |
∴b<
| 3 |
| 2 |
又∵a,b∈N*,
∴b=1,a=1;
(Ⅱ)由(1)得f(x)=x-
| 1 |
| x+1 |
函数在(-1,+∞)单调递增.
证明:任取x1,x2且-1<x1<x2,
f(x1)-f(x2)=x1-
| 1 |
| x1+1 |
| 1 |
| x2+1 |
| 1 |
| x2+1 |
| 1 |
| x1+1 |
=(x1-x2)+
| x1-x2 |
| (x1+1)(x2+1) |
| 1 |
| (x1+1)(x2+1) |
∵-1<x1<x2,
∴x1-x2<0,1+
| 1 |
| (x1+1)(x2+1) |
∴(x1-x2)[1+
| 1 |
| (x1+1)(x2+1) |
即f(x1)<f(x2),
故函数f(x)=x-
| 1 |
| x+1 |
点评:本题考察了函数的单调性,导数的应用,求参数的范围,不等式的证明,是一样的综合题.

练习册系列答案
相关题目
 如图,已知正方形ABCD和ADMN边长都为2,且平面ABCD⊥平面ADMN,E是BC的中点,F是MD的中点,
如图,已知正方形ABCD和ADMN边长都为2,且平面ABCD⊥平面ADMN,E是BC的中点,F是MD的中点, 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=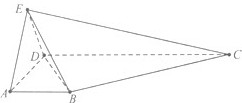 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=