题目内容

已知四面体P-ABC中，PA=4，AC=2
7
，PB=BC=2
3
，PA⊥平面PBC，则四面体P-ABC的内切球半径与外接球半径的比（　　）
A、
3
2
16
B、
3
2
8
C、
2
16
D、
2
8
考点：直线与平面垂直的判定
专题：计算题,空间位置关系与距离
分析：确定△PBC为等边三角形，△ABC为等腰三角形，分别求出四面体P-ABC的内切球半径与外接球半径，即可得出结论．
解答： 解：由题意，已知PA⊥面PBC，PA=4，PB=BC=2
3
，AC=2
7
，
所以，由勾股定理得到：AB=2
7
，PC=2
3
，
所以，△PBC为等边三角形，△ABC为等腰三角形，
等边三角形PBC所在的小圆的直径PD=
2
3
sin60°
=4，
那么，四面体P-ABC的外接球直径2R=
16+16
=4
2
，所以，R=2
2
，
VP-ABC=
1
3
S△PBC•PA=
1
3
•
3
4
•12•4=4
3
，
表面积S=
1
2
•2
3
•4•2+
3
4
•12+
1
2
•2
3
•5=16
3
，
设内切球半径为r，那么4
3
=
1
3
•16
3
r，所以r=
3
4
，
所以四面体P-ABC的内切球半径与外接球半径的比
3
4
2
2
=
3
2
16
．
故选：A．
点评：本题考查四面体P-ABC的内切球半径与外接球半径，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=1-ax，g（x）=x-
2
x+1
，若?x1∈[1，2]，总?x2∈[0，1]使f（x1）=g（x2），求实数a的取值范围．
求值：
（1）2cos
π
2
-tan
π
4
+
3
4
tan2
π
6
-sin
π
6
+cos2
π
6
+sin
3π
2

（2）sin2
π
3
+cos4
3π
2
-tan2
π
3
．
己知直线l经过两点P1（x1，y1），P2（x2，y2）（x1≠x2），则直线l的方程为：
y-y1
x-x1
=
y2-y1
x2-x1
，由于这个方程
 
确定的，因此这个方程叫做直线的
 
方程．
已知函数f（x）=x2，其值域是M={0，1，9}，则其定义域可能有几个？
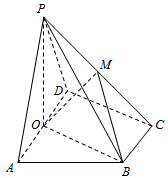在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=
1
2
AD=1，CD=
3
．
（Ⅰ）求证：平面MQB⊥平面PAD；
（Ⅱ）若二面角M-BQ-C大小为60°，求QM的长．
若直线y=kx-k交抛物线y2=4x于A，B两点，且线段AB中点到y轴的距离为3，则|AB|=（　　）
A、12B、10C、8D、6
已知f（x）是定义在R上的函数，f（1）=1，且?x1，x2∈R，总有f（x1+x2）=f（x1）+f（x2）+1恒成立．
（Ⅰ）记g（x）=f（x）+1，求证：g（x）是奇函数；
（Ⅱ）对?n∈N*，有an=
1
f(n)
，bn=f（
1
2n+1
）+1，记cn=
bn
an
，求{cn}的前n项和Sn；
（Ⅲ）求F（n）=an+1+an+2+…+a2n（n≥2，n∈N）的最小值．
在直角梯形ABCD中，AD∥BC，BC=2AD=2AB=2
2
，∠ABC=90°，如图，把△ABD沿BD翻折，使得平面ABD⊥平面BCD．

（Ⅰ）求证：CD⊥AB；
（Ⅱ）若点M为线段BC中点，求点M到平面ACD的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网