题目内容
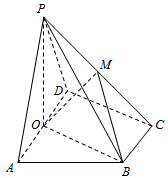 在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=| 1 |
| 2 |
| 3 |
(Ⅰ)求证:平面MQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C大小为60°,求QM的长.
考点:平面与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由题意易证QB⊥AD,由面面垂直的性质可得BQ⊥平面PAD,由此能证明平面MQB⊥平面PAD.
(Ⅱ)求出平面BQC的法向量和平面MBQ法向量,结合题意可得λ的方程,解方程可得λ,可得QM的长.
(Ⅱ)求出平面BQC的法向量和平面MBQ法向量,结合题意可得λ的方程,解方程可得λ,可得QM的长.
解答:
 解:(Ⅰ)∵AD∥BC,BC=
解:(Ⅰ)∵AD∥BC,BC=
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ
又∵∠ADC=90°,∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.∵BQ?平面PQB,
∴平面PQB⊥平面PAD.
(Ⅱ)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则Q(0,0,0),B(0,
,0),C(-1,
,0),P(0,0,
),
∵M是PC中点,∴M(-
,
,
),
∴
=(-
,-
,
),
=(0,0,
),
=(-1,
,0),
设
=λ
+(1-λ)
,
∵0≤λ≤1,∴
=(λ-1,
(1-λ),
λ),
=(0,
,0),
设平面BQM的法向量
=(x,y,z),
则
,
取x=
,得平面MBQ法向量为
=(
,0,
),
平面BQC的法向量为
=(0,0,1),
∵二面角M-BQ-C为60°,∴cos60°=
=
=
,
∴解得λ=
,∴
=(-
,
,
),
|
|=
=
.
 解:(Ⅰ)∵AD∥BC,BC=
解:(Ⅰ)∵AD∥BC,BC=| 1 |
| 2 |
∴四边形BCDQ为平行四边形,∴CD∥BQ
又∵∠ADC=90°,∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.∵BQ?平面PQB,
∴平面PQB⊥平面PAD.
(Ⅱ)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则Q(0,0,0),B(0,
| 3 |
| 3 |
| 3 |
∵M是PC中点,∴M(-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| BM |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| QP |
| 3 |
| QC |
| 3 |
设
| QM |
| QP |
| QC |
∵0≤λ≤1,∴
| QM |
| 3 |
| 3 |
| QB |
| 3 |
设平面BQM的法向量
| m |
则
|
取x=
| 3 |
| m |
| 3 |
| 1-λ |
| λ |
平面BQC的法向量为
| n |
∵二面角M-BQ-C为60°,∴cos60°=
|
| ||||
|
|
| ||||
|
| 1 |
| 2 |
∴解得λ=
| 1 |
| 2 |
| QM |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
|
| QM |
|
| ||
| 2 |
点评:本题考查面面垂直的证明,考查使得二面为60°的线段长的求法,考查向量法在立体几何中的应用,考查方程思想、等价转化思想等数学思想方法和学生的空间想象能力、逻辑推理能力和运算求解能力,是中档题.

练习册系列答案
相关题目
若函数f(x)=2sin2x+2
sinxcosx+1,则函数f(x)的最小正周期为( )
| 3 |
| A、2π | ||
B、
| ||
| C、π | ||
D、
|
已知函数y=lg(-sinθ)+lgcosθ,则θ角在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设a>b>0,a+b=1且x=ba,y=ab,z=log
a则x,y,z之间的大小关系是( )
| 1 |
| b |
| A、y<x<z |
| B、y<z<x |
| C、z<y<x |
| D、z<x<y |
已知四面体P-ABC中,PA=4,AC=2
,PB=BC=2
,PA⊥平面PBC,则四面体P-ABC的内切球半径与外接球半径的比( )
| 7 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知过定点P(2,0)的直线l与曲线y=
相交于A,B两点,O为坐标原点,当S△AOB=1时,直线l的倾斜角为( )
| 2-x2 |
| A、150° | B、135° |
| C、120° | D、不存在 |
椭圆
+y2=1两个焦点分别是F1,F2,点P是椭圆上任意一点,则
•
的取值范围是( )
| x2 |
| 4 |
| PF1 |
| PF2 |
| A、[1,4] |
| B、[1,3] |
| C、[-2,1] |
| D、[-1,1] |