题目内容
20．△ABC中，已知点A（2，1），B（-2，3），C（0，1），则BC边上的中线所在直线的一般式方程为x+y-3=0．分析 利用中点坐标公式、点斜式即可得出．
解答 解：线段BC的中点为M（-1，2），
∴KBM=$\frac{2-3}{-1-（-2）}$=-1
∴BC边上的中线所在的直线方程为y-2=-（x+1），
化为：x+y-3=0，
故答案为：x+y-3=0．
点评 本题考查了中点坐标公式、点斜式方程，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
10．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+ax-2，}&{x≤1}\\{lo{g}_{a}x，}&{x＞1}\end{array}\right.$在R上单调递增，则实数a的取值范围是（ ）
| A． | 0＜a≤3 | B． | a≥2 | C． | 2≤a≤3 | D． | 0＜a≤2或a≥3 |
8．已知a，b，c为非零常数，则下列命题正确的是（ ）
| A． | 若a＜b，则a2＜b2 | B． | 若a＜b，则ac＜bc | C． | 若a＞b，则ac2＞bc2 | D． | 若a＞b，则$\frac{1}{a}$＜$\frac{1}{b}$ |
5．已知a，b是两条直线，α是一个平面，则下列判断正确的是（ ）
| A． | a⊥α，b⊥α，则a⊥b | B． | a∥α，b?α，则a∥b | ||
| C． | a⊥b，b?α，则a⊥α | D． | a∥α，b?α，a?α，则a∥α |
12．
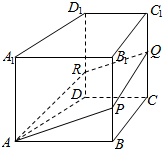如图，在四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD，AB∥CD，∠DCB=90°，AB=AD=AA1=2DC，Q为棱CC1上一动点，过直线AQ的平面分别与棱BB1，DD1交于点P，R，则下列结论错误的是（ ）
如图，在四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD，AB∥CD，∠DCB=90°，AB=AD=AA1=2DC，Q为棱CC1上一动点，过直线AQ的平面分别与棱BB1，DD1交于点P，R，则下列结论错误的是（ ）| A． | 对于任意的点Q，都有AP∥QR | |
| B． | 对于任意的点Q，四边形APQR不可能为平行四边形 | |
| C． | 存在点Q，使得△ARP为等腰直角三角形 | |
| D． | 存在点Q，使得直线BC∥平面APQR |
在空间四边形ABCD中，E、F、O、H分别是AB、BC、CD、DA的中点，且AC=BD，求证：EO与FH互相垂直平分．