题目内容
9.已知f(x)为定义在R上的奇函数,当x>0时,f(x)为二次函数,且满足f(2)=1,f(x)在(0,+∞)上的两个零点为1和3.(1)求函数f(x)在R上的解析式;
(2)若x∈(-∞,m),函数f(x)的图象恒在y=-3的上方,求m的取值范围.
分析 (1)设出x>0的f(x)的解析式,由f(2)=1,求得系数,得到解析式;再由奇函数的定义,即可得到所求f(x)的解析式;
(2)由题意可得x∈(-∞,m)时,f(x)的最小值大于-3.讨论x<0时的最大值,以及x>0时,f(x)=-3的解,结合图象即可得到所求m的范围.
解答  解:(1)由题意,当x>0时,设f(x)=a(x-1)(x-3)(a≠0),
解:(1)由题意,当x>0时,设f(x)=a(x-1)(x-3)(a≠0),
∵f(2)=1,∴a=-1,∴f(x)=-x2+4x-3,
当x<0时,-x>0,∵f(x)为R上的奇函数,
∴f(-x)=-f(x),
∴f(x)=-f(-x)=-[-(-x)2+4(-x)-3]=x2+4x+3,
即x<0时,f(x)=x2+4x+3,
当x=0时,由f(-x)=-f(x)得:f(0)=0,
所以f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x-3,x>0}\\{0,x=0}\\{{x}^{2}+4x+3,x<0}\end{array}\right.$;
(2)作出f(x)的图象(如图所示)
由x∈(-∞,m),函数f(x)的图象恒在y=-3的上方,
可得x∈(-∞,m)时,f(x)的最小值大于-3.
当x<0时,f(x)=x2+4x+3在x=-2处取得最小值,且为-1;
当x>0时,f(x)=-x2+4x-3的图象开口向下,
令-x2+4x-3=-3,解得x=0或4,
综上可得,m的范围是m≤4.
点评 本题考查函数的解析式的求法,注意运用函数的奇偶性和待定系数法,考查不等式恒成立问题的解法,运用转化思想和结合图象是解题的关键.

练习册系列答案
相关题目
19.函数f(x)=(1-x)|x-3|在(-∞,a]上取得最小值-1,则实数a的取值范围是( )
| A. | (-∞,2] | B. | $[{2-\sqrt{2},\;2}]$ | C. | $[{2,\;2+\sqrt{2}}]$ | D. | [2,+∞) |
17.下列命题中正确的个数为( )
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②残差平方和越小的模型,模型拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好.
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②残差平方和越小的模型,模型拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
4.已知m,n为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )
| A. | m∥n,m⊥α⇒n⊥α | B. | α∥β,m?α,n?β⇒m∥n | ||
| C. | m?α,n?β,m∥n⇒α∥β | D. | m?α,n?α,m∥β,n∥β⇒α∥β |
1.在平面直角坐标系中,已知A(1,0),B(3,2),则直线AB的倾斜角大小( )
| A. | 30° | B. | 45° | C. | 135° | D. | 150° |
18.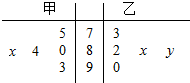 在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )
在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )
 在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )
在学校组织的“国学经典”朗诵比赛中,5位评委对甲、乙两名同学的评分如茎叶图所示(满分100分),若甲同学所得评分的众数为84,则甲同学所得评分的平均数不大于乙同学所得评分的平均数的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |