题目内容
1.若集合M={y∈N|y<6},N={x|log2(x-1)≤2},则M∩N=( )| A. | (1,5] | B. | (-∞,5] | C. | {1,2,3,4,5} | D. | {2,3,4,5} |
分析 分别求出集合M,N,由此能求出M∩N的值.
解答 解:∵集合M={y∈N|y<6}={0,1,2,3,4,5},
N={x|log2(x-1)≤2}={x|1<x≤5},
∴M∩N={2,3,4,5}.
故选:D.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
11.将函数y=sin(x-$\frac{π}{12}$)图象上的点P($\frac{π}{4}$,t)向左平移s(s>0)个单位,得到点P′,若P′位于函数y=sin2x的图象上,则( )
| A. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{6}$ | B. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{6}$ | ||
| C. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{12}$ | D. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{12}$ |
12.已知集合A={x|x2-3x+2<0},B={x|3-x>0},则A∩B=( )
| A. | (2,3) | B. | (1,3) | C. | (1,2) | D. | (-∞,3) |
16.定义在R上的奇函数y=f(x)为减函数,若m,n满足f(m2-2m)+f(2n-n2)≤0,则当1≤n≤$\frac{3}{2}$时,$\frac{m}{n}$的取值范围为( )
| A. | [-$\frac{2}{3}$,1] | B. | [1,$\frac{3}{2}$] | C. | [$\frac{1}{3}$,$\frac{3}{2}$] | D. | [$\frac{1}{3}$,1] |
6.从区间[0,1]随机选取三个数x,y,z,若满足x2+y2+z2>1,则记参数t=1,否则t=0,在进行1000次重复试验后,累计所有参数的和为477,由此估算圆周率π的值应为( )
| A. | 3.084 | B. | 3.138 | C. | 3.142 | D. | 3.136 |
13.2017是等差数列4,7,10,13,…的第几项( )
| A. | 669 | B. | 670 | C. | 671 | D. | 672 |
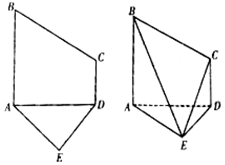 已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.
已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成,如图所示,AB⊥AD,AE⊥DE,AB∥CD,且AB=2CD=2DE=4,将五边形ABCDE沿着AD折起,且使平面ABCD⊥平面ADE.