题目内容
13．已知正四棱锥的高为4，侧棱长为3$\sqrt{2}$，则该棱锥的体积为$\frac{16}{3}$．分析 作出棱锥的直观图，利用勾股定理求出棱柱的底面对角线的长，进而求出底面边长，得出棱锥的体积．
解答 
解：∵正四棱锥P-ABCD，∴底面ABCD是正方形，作PO⊥平面ABCD，则O为正方形ABCD的中心，
∵PO=4，PA=3$\sqrt{2}$，∴OA=$\sqrt{P{A}^{2}-P{O}^{2}}$=$\sqrt{2}$，∴AC=2OA=2$\sqrt{2}$，∴AB=2，
∴V=$\frac{1}{3}$×22×4=$\frac{16}{3}$．
故答案为$\frac{16}{3}$．
点评 本题考查了棱锥的结构特征，棱锥的体积计算，属于中档题．
练习册系列答案
相关题目
3．已知正三棱锥的正视图和俯视如图所示，则其侧视图的面积为（ ）
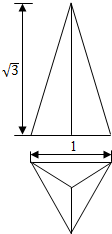
| A． | $\frac{\sqrt{3}}{4}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{3}{4}$ | D． | 1 |
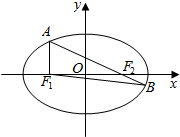如图，点F1，F2分别是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点．点A是椭圆C上一点，点B是直线AF2与椭圆C的另一交点，且满足AF1⊥x轴，∠AF2F1=30°．
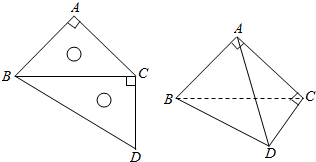一副三角板如图拼成，AB=AC，∠BAC=90°，∠DBC=30°，∠BCD=90°，将△BCD沿BC折起，使得平面ABC⊥平面BCD．
在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别为A1D1和A1B1的中点．
3．点A是椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞1）的上顶点，B、C是该椭圆的另外两点，且△ABC是以点A为直角顶点的等腰直角三角形，若满足条件的△ABC只有一个，则椭圆的离心率e的范围是（ ）
| A． | $\frac{\sqrt{3}}{3}$≤e＜1 | B． | 0＜e≤$\frac{\sqrt{3}}{3}$ | C． | 0＜e≤$\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{6}}{3}$≤e＜1 |