题目内容
17.已知F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两焦点,过F1且垂直于x轴的直线交椭圆于P,Q两点,若△PQF2为正三角形,则椭圆的离心率是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 先求出PF1 的长,直角三角形PF1F2 中,由边角关系得tan30°=$\frac{P{F}_{1}}{{F}_{1}{F}_{2}}$=$\frac{\frac{{b}^{2}}{a}}{2c}$,建立关于离心率的方程,解方程求出离心率的值
解答 解:由已知可得,PF1=$\frac{{b}^{2}}{a}$
∵tan30°=$\frac{P{F}_{1}}{{F}_{1}{F}_{2}}$=$\frac{\frac{{b}^{2}}{a}}{2c}$=$\frac{1-{e}^{2}}{2e}$=$\frac{\sqrt{3}}{3}$
∴$\sqrt{3}{e}^{2}+2e-\sqrt{3}=0$
∵0<e<1
∴e=$\frac{\sqrt{3}}{3}$
故选:D.
点评 本题考查椭圆的简单性质,直角三角形中的边角关系,解方程求离心率的大小.

练习册系列答案
相关题目
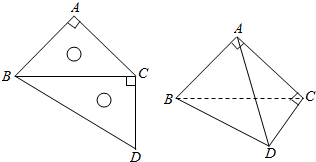 一副三角板如图拼成,AB=AC,∠BAC=90°,∠DBC=30°,∠BCD=90°,将△BCD沿BC折起,使得平面ABC⊥平面BCD.
一副三角板如图拼成,AB=AC,∠BAC=90°,∠DBC=30°,∠BCD=90°,将△BCD沿BC折起,使得平面ABC⊥平面BCD.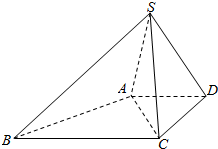 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2. 在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.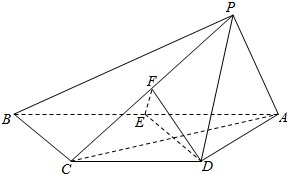 如图,四棱锥P-ABCD中,AP⊥平面PBC,AB∥DC,AP=AD=DC=$\frac{1}{2}$AB=1,∠ADC=120°,E,F分别为线段AB,PC的中点.
如图,四棱锥P-ABCD中,AP⊥平面PBC,AB∥DC,AP=AD=DC=$\frac{1}{2}$AB=1,∠ADC=120°,E,F分别为线段AB,PC的中点.