题目内容
20.已知椭圆C的左、右焦点分别为F1,F2,过F2的直线与椭圆相交于P,Q两点,若PQ⊥PF1,且4PF1=3PQ,则椭圆的离心率e=$\frac{\sqrt{2}}{2}$.分析 设|QF2|=m,|PF2|=n,利用椭圆的定义可得|QF1|=2a-m,|PF1|=2a-n.由4|PF1|=3|PQ|,可得4(2a-n)=3(m+n).由PF1⊥PQ,利用勾股定理可得:(2a-n)2+n2=4c2,(2a-n)2+(m+n)2=(2a-m)2.联立解得即可.
解答 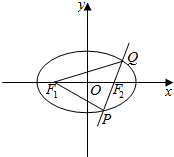 解:如图所示,设|QF2|=m,|PF2|=n,
解:如图所示,设|QF2|=m,|PF2|=n,
则|QF1|=2a-m,|PF1|=2a-n.
∵4|PF1|=3|PQ|,∴4(2a-n)=3(m+n),
∵PF1⊥PQ,
∴(2a-n)2+n2=4c2,
(2a-n)2+(m+n)2=(2a-m)2.
联立$\left\{\begin{array}{l}{4(2a-n)=3(n+m)}\\{(2a-n)^{2}+{n}^{2}=4{c}^{2}}\\{(2a-n)^{2}+(m+n)^{2}=(2a-m)^{2}}\end{array}\right.$,
化为n=a,代入可得a2=2c2.
解得e=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了椭圆的定义及其性质、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
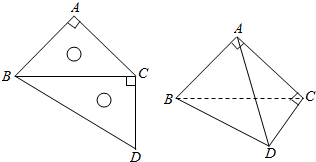 一副三角板如图拼成,AB=AC,∠BAC=90°,∠DBC=30°,∠BCD=90°,将△BCD沿BC折起,使得平面ABC⊥平面BCD.
一副三角板如图拼成,AB=AC,∠BAC=90°,∠DBC=30°,∠BCD=90°,将△BCD沿BC折起,使得平面ABC⊥平面BCD.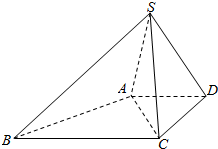 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,AD=DC=$\sqrt{2}$,SA=SC=SD=2.