题目内容
13.在△ABC中,D为边BC上一点,tan∠BAD=$\frac{1}{3}$,tan∠CAD=$\frac{1}{2}$,AB=$\sqrt{2}$AC,BC=3,则AD=( )| A. | $\frac{7}{2}$ | B. | $\frac{{3\sqrt{5}}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
分析 由两角和与差的正切函数推知∠BAC=45°,结合余弦定理求得AC的长度,由此推知△ABC为直角三角形;然后在直角△ACD中利用勾股定理来求AD的长度即可.
解答 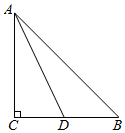 解:如图,∵tan∠BAD=$\frac{1}{3}$,tan∠CAD=$\frac{1}{2}$,
解:如图,∵tan∠BAD=$\frac{1}{3}$,tan∠CAD=$\frac{1}{2}$,
∴tan∠BAC=tan(∠BAD+∠CAD)=$\frac{tan∠BAD+tan∠CAD}{1-tan∠BAD•tan∠CAD}$=$\frac{\frac{1}{3}+\frac{1}{2}}{1-\frac{1}{3}×\frac{1}{2}}$=1,
∵0<∠BAC<180°,
∴∠BAC=45°.
∴cos∠BAC=$\frac{A{C}^{2}+A{B}^{2}-B{C}^{2}}{2AC•AB}$=$\frac{A{C}^{2}+2A{C}^{2}-9}{2×AC×\sqrt{2}AC}$=$\frac{\sqrt{2}}{2}$,则AC=3,
∴AC=BC=3,
∴∠BAC=∠B=45°,
∴∠C=90°.
∴tan∠CAD=$\frac{CD}{AC}$=$\frac{CD}{3}$=$\frac{1}{2}$,
∴CD=$\frac{3}{2}$,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\frac{3\sqrt{5}}{2}$.
故选:B.
点评 本题考查了两角和与差的正切函数,余弦定理以及勾股定理,本题难度不大,熟记公式即可解答该题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知抛物线y=x2的焦点为F,过点(0,2)作直线l与抛物线交于A,B两点,点F关于直线OA的对称点为C,则四边形OCAB面积的最小值为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
8.某酒厂生产A、B两种优质白酒,生产每吨白酒所需的主要原料如表:
已知每吨A白酒的利润是7万元,每吨B白酒的利润是12万元,由于条件限制,该酒厂目前库存高粱360吨,大米300吨,小麦200吨.
(Ⅰ)设生产A、B两种白酒分别为x吨、y吨,总利润为z万元,请列出满足上述条件的不等式组及目标函数;
(Ⅱ)生产A、B两种白酒各多少吨,才能获得最大利润?并求出最大利润.
| 白酒品种 | 高粱(吨) | 大米(吨) | 小麦(吨) |
| A | 9 | 3 | 4 |
| B | 4 | 10 | 5 |
(Ⅰ)设生产A、B两种白酒分别为x吨、y吨,总利润为z万元,请列出满足上述条件的不等式组及目标函数;
(Ⅱ)生产A、B两种白酒各多少吨,才能获得最大利润?并求出最大利润.
5.已知集合M={1,2,3,4,5},N={0,2,4},P=M∩N,则P的子集共有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
2.设数列{an}为等差数列,{bn}为等比数列,若a1<a2,b1<b2,且bi=a${\;}_{i}^{2}$(i=1,2,3),则数列{bn}的公比为( )
| A. | 1+2$\sqrt{2}$ | B. | 3+2$\sqrt{2}$ | C. | 3-2$\sqrt{2}$ | D. | 2$\sqrt{2}$-1 |