题目内容
3.已知抛物线y=x2的焦点为F,过点(0,2)作直线l与抛物线交于A,B两点,点F关于直线OA的对称点为C,则四边形OCAB面积的最小值为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
分析 设直线AB方程为y=kx+2,联立y=x2求解,设d1、d2分别为F到OA、O到AB的距离,利用四边形OCAB的面积S=S△OAC+S△OAB=$\frac{1}{2}$(OA•d1+AB•d2),可得S关于k的函数,利用导数知识即可求解.
解答 解:不妨设位于第一象限的交点为A(x1,y1)、第二象限的交点为B(x2,y2),则x1>0,x2<0.OA的直线方程为y=$\frac{{y}_{1}}{{x}_{1}}$x=x1x,F点的坐标为(0,$\frac{1}{4}$).
设直线AB方程为y=kx+2,联立y=x2求解,有x2-kx-2=0
∴x1+x2=k,x1x2=-2,△=k2+8,x1=$\frac{1}{2}$(k+$\sqrt{{k}^{2}+8}$)①;线段AB=$\sqrt{(1+{k}^{2})({k}^{2}+8)}$②.
设d1、d2分别为F到OA、O到AB的距离.
∵C是F关于OA的对称点,∴C到OA的距离=d1.
∴四边形OCAB的面积S=S△OAC+S△OAB=$\frac{1}{2}$(OA•d1+AB•d2).
根据点到直线距离公式,d1=$\frac{\frac{1}{4}}{\sqrt{1+{{x}_{1}}^{2}}}$③,d2=$\frac{2}{\sqrt{1+{k}^{2}}}$④.
又线段OA=${x}_{1}\sqrt{1+{{x}_{1}}^{2}}$⑤,
∴将①~⑤代入S,有S=$\frac{1}{16}$(k+17$\sqrt{{k}^{2}+8}$).
由S对k求导,令导函数=0,可得1+$\frac{17k}{\sqrt{{k}^{2}+8}}$=0,解得k=-$\frac{1}{6}$时,S最小,其值为3.
故选:D.
点评 本题考查抛物线的简单性质,考查面积的计算,考查导数知识,正确求出面积,利用导数求解是解题的关键.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| A. | (-∞,-1) | B. | (-1,1) | C. | (-∞,0) | D. | (-1,+∞) |
| A. | y=±$\frac{\sqrt{10}}{2}$x | B. | y=±$\frac{\sqrt{6}}{2}$x | C. | y=±$\sqrt{6}$x | D. | y=±$\sqrt{10}$x |
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ |
| A. | $\frac{1}{2}$(3n-1) | B. | $\frac{1}{2}$(3n+1) | C. | 3n | D. | 3n+1 |
| A. | $\frac{7}{2}$ | B. | $\frac{{3\sqrt{5}}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
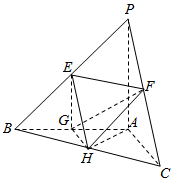 如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2.
如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2.