题目内容
5.在直角坐标系xOy中,曲线C1的方程为$\frac{x^2}{9}+{y^2}=1$.以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2-8ρsinθ+15=0.(Ⅰ)写出C1的参数方程和C2的直角坐标方程;
(Ⅱ)设点P在C1上,点Q在C2上,求|PQ|的最大值.
分析 (Ⅰ)利用三种方程的转化方法,写出C1的参数方程和C2的直角坐标方程;
(Ⅱ)设P(3cosα,sinα),则|PC2|=$\sqrt{(3cosα-4)^{2}+si{n}^{2}α}$=$\sqrt{8(cosα-\frac{3}{2})^{2}-1}$,即可求|PQ|的最大值.
解答 解:(Ⅰ)曲线C1的方程为$\frac{x^2}{9}+{y^2}=1$,参数方程为$\left\{\begin{array}{l}{x=3cosα}\\{y=sinα}\end{array}\right.$(α为参数).
曲线C2的极坐标方程为ρ2-8ρsinθ+15=0,直角坐标方程为x2+y2-8y+15=0,即(x-4)2+y2=1;
(Ⅱ)设P(3cosα,sinα),则|PC2|=$\sqrt{(3cosα-4)^{2}+si{n}^{2}α}$=$\sqrt{8(cosα-\frac{3}{2})^{2}-1}$,
∴cosα=-1,|PC2|max=7,
∴|PQ|的最大值为7+1=8.
点评 本题考查三种方程的转化,考查参数方程的运用,考查三角函数知识,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
15.设偶函数y=2sin(ωx+φ)(ω>0,0<φ<π)的图象与直线y=2的某两个交点的横坐标分别为x1,x2,若|x2-x1||的最小值为π,则该函数在下列哪个区间上单调递增( )
| A. | (0,$\frac{π}{2}$) | B. | (-$\frac{π}{4}$,$\frac{π}{4}$) | C. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | D. | ($\frac{π}{4}$,$\frac{3π}{4}$) |
13.下面四个残差图中可以反映出回归模型拟合精度较好的为( )


| A. | 图1 | B. | 图2 | C. | 图3 | D. | 图4 |
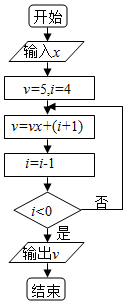 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )