题目内容
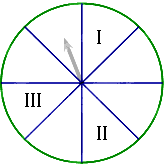
某电视台“挑战60秒”活动规定上台演唱：（Ⅰ）连续达到60秒可转动转盘（转盘为八等分圆盘）一次进行抽奖，达到90秒可转两次，达到120秒可转三次（奖金累加）．
（Ⅱ）转盘指针落在Ⅰ、Ⅱ、Ⅲ区依次为一等奖（500元）、二等奖（200元）、三等奖（100元），落在其它区域不奖励．
（Ⅲ）演唱时间从开始到三位评委中至少1人呜啰为止，现有一演唱者演唱时间为100秒．
（1）求此人中一等奖的概率；
（2）设此人所得奖金为ξ，求ξ的分布列及数学期望Eξ．
考点：离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题：概率与统计
分析：（1）利用相互独立事件的概率乘法公式能求出此人中一等奖的概率．
（2）此人所得奖金ξ的所有可能取值为0，100，200，300，400，500，600，700，1000，分别求出相应的概率，能求出ξ的分布列及数学期望Eξ．
（2）此人所得奖金ξ的所有可能取值为0，100，200，300，400，500，600，700，1000，分别求出相应的概率，能求出ξ的分布列及数学期望Eξ．
解答：
解：（1）此人中一等奖的概率：
p=
×
+
×
+
×
=
．
（2）此人所得奖金ξ的所有可能取值为0，100，200，300，400，500，600，700，1000，
P（ξ=0）=
×
=
，P（ξ=100）=
×
+
×
=
，
P（ξ=200）=
×
+
×
+
×
=
，P（ξ=300）=
×
+
×
=
，
P（ξ=400）=
×
=
，P（ξ=500）=
×
+
×
=
，
P（ξ=600）=
×
+
×
=
，P（ξ=700）=
×
+
×
=
，P（ξ=1000=
×
=
，
∴ξ的分布列为：
∴Eξ=100×
+200×
+300×
+400×
+500×
+600×
+700×
+1000×
=200．
p=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
| 1 |
| 8 |
| 15 |
| 64 |
（2）此人所得奖金ξ的所有可能取值为0，100，200，300，400，500，600，700，1000，
P（ξ=0）=
| 5 |
| 8 |
| 5 |
| 8 |
| 25 |
| 64 |
| 1 |
| 8 |
| 5 |
| 8 |
| 5 |
| 8 |
| 1 |
| 8 |
| 10 |
| 64 |
P（ξ=200）=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 5 |
| 8 |
| 5 |
| 8 |
| 1 |
| 8 |
| 11 |
| 64 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 2 |
| 64 |
P（ξ=400）=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 64 |
| 1 |
| 8 |
| 5 |
| 8 |
| 5 |
| 8 |
| 1 |
| 8 |
| 10 |
| 64 |
P（ξ=600）=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 2 |
| 64 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 2 |
| 64 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 64 |
∴ξ的分布列为：
| ξ | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 1000 | ||||||||||||||||||
| P |
|
|
|
|
|
|
|
|
|
| 10 |
| 64 |
| 11 |
| 64 |
| 2 |
| 64 |
| 1 |
| 64 |
| 10 |
| 64 |
| 2 |
| 64 |
| 2 |
| 64 |
| 1 |
| 64 |
点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，在历年高考中都是必考题型．
练习册系列答案
科学实验活动册系列答案
相关题目