题目内容
18.$函数f(x)={log_2}(4-{x^2})的$值域为(-∞,2],不等式f(x)<1的解集为(-2,-$\sqrt{2}$)∪($\sqrt{2}$,2).分析 根据4-x2的范围和对数函数的单调性求出f(x)的值域,利用单调性得出0<4-x2<2,解出解集.
解答 解:∵0<4-x2≤4,∴log2(4-x2)≤log24=2.
令log2(4-x2)<1得0<4-x2<2,解得-2<x<-$\sqrt{2}$或$\sqrt{2}$<x<2.
故答案为(-∞,2],(-2,-$\sqrt{2}$)∪($\sqrt{2}$,2).
点评 本题考查了对数函数的性质,单调性的应用,属于基础题.

练习册系列答案
相关题目
16.若实数x,y满足$\sqrt{{x}^{2}+(y-13)^{2}}$-$\sqrt{{x}^{2}+(y+13)^{2}}$=10,则动点P(x,y)的轨迹方程是( )
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1(x>0) | B. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{144}$=1(x<0) | ||
| C. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1(y>0) | D. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{144}$=1(y<0) |
3.△ABC的三边长度分别是2,3,x,由所有满足该条件的x构成集合M,现从集合M中任取一x值,所得△ABC恰好是钝角三角形的概率为( )
| A. | $\frac{{4-\sqrt{13}+\sqrt{5}}}{4}$ | B. | $\frac{{5-\sqrt{13}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{5}-1}}{4}$ |
8.函数f(x)=cos2(x-$\frac{π}{4}$)-cos2(x+$\frac{π}{4}$)的最大值和最小正周期分别为( )
| A. | $\frac{1}{2}$,π | B. | 1,π | C. | $\frac{1}{2}$,$\frac{π}{2}$ | D. | 1,$\frac{π}{2}$ |
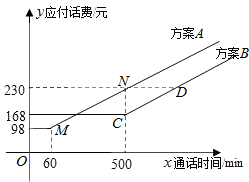 电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为($\frac{2120}{3}$,230).
电信局为了配合客户不同需要,设有A,B两种优惠方案.这两种方案应付话费(元)与通话时间x(min)之间的关系如图所示,其中D的坐标为($\frac{2120}{3}$,230). 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,