题目内容
3.△ABC的三边长度分别是2,3,x,由所有满足该条件的x构成集合M,现从集合M中任取一x值,所得△ABC恰好是钝角三角形的概率为( )| A. | $\frac{{4-\sqrt{13}+\sqrt{5}}}{4}$ | B. | $\frac{{5-\sqrt{13}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{5}-1}}{4}$ |
分析 根据△ABC的三边长度分别是2,3,x,$\left\{\begin{array}{l}{2+3>x}\\{2+x>3}\end{array}\right.$,1<x<5,区间长度为4,△ABC恰好是钝角三角形$\left\{\begin{array}{l}{4+{x}^{2}-9<0}\\{4+9-{x}^{2}<0}\\{2+3>x}\\{2+x>3}\end{array}\right.$,x的取值范围是(1,$\sqrt{5}$)∪($\sqrt{13}$,5),区间长度为(4-$\sqrt{13}$+$\sqrt{5}$),即可求出概率.
解答 解:由题意,△ABC的三边长度分别是2,3,x,$\left\{\begin{array}{l}{2+3>x}\\{2+x>3}\end{array}\right.$,∴1<x<5,区间长度为4,
△ABC恰好是钝角三角形$\left\{\begin{array}{l}{4+{x}^{2}-9<0}\\{4+9-{x}^{2}<0}\\{2+3>x}\\{2+x>3}\end{array}\right.$,
∴x的取值范围是(1,$\sqrt{5}$)∪($\sqrt{13}$,5),区间长度为(4-$\sqrt{13}$+$\sqrt{5}$),
∴从集合M中任取一x值,所得△ABC恰好是钝角三角形的概率为$\frac{4-\sqrt{13}+\sqrt{5}}{4}$.
故选:A.
点评 此题考查学生灵活运用余弦定理化简求值,会求一元二次不等式组的解集,是一道综合题.学生在做题时应注意钝角三角形这个条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知定义在R上的函数f(x)满足:f(x+y)=f(x)+f(y)+1,若f(8)=15,则f(2)=( )
| A. | $\frac{15}{4}$ | B. | 3 | C. | 2 | D. | -1 |
12.设m,n∈(0,+∞),若直线(m+2)x+(n+2)y-4=0与圆(x-1)2+(y-1)2=1相切,则m+n的最小值是( )
| A. | 4+4$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 4+$\sqrt{2}$ | D. | 4+2$\sqrt{2}$ |
13.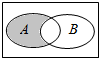 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )| A. | {2,3,4} | B. | {2,3,4,5} | C. | {3,4} | D. | {3,4,5} |
 已知函数f(x)=|x+1|+|x-3|.
已知函数f(x)=|x+1|+|x-3|.