题目内容
8.函数f(x)=cos2(x-$\frac{π}{4}$)-cos2(x+$\frac{π}{4}$)的最大值和最小正周期分别为( )| A. | $\frac{1}{2}$,π | B. | 1,π | C. | $\frac{1}{2}$,$\frac{π}{2}$ | D. | 1,$\frac{π}{2}$ |
分析 使用诱导公式对f(x)进行化简,
解答 解:f(x)=cos2[$\frac{π}{2}$-(x+$\frac{π}{4}$)]-cos2(x+$\frac{π}{4}$)=sin2(x+$\frac{π}{4}$)-cos2(x+$\frac{π}{4}$)=-cos(2x+$\frac{π}{2}$)=sin2x.
∴f(x)的最大值为1,周期T=$\frac{2π}{2}$=π.
故选:B.
点评 本题考查了三角函数的恒等变换和正弦函数的性质,观察两角的关系,用一个角表示出另一个角是解题关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知函数f(x)=lnx+2sinα(α∈(0,$\frac{π}{2}$))的导函数f′(x),若存在x0<1使得f′(x0)=f(x0)成立,则实数α的取值范围为( )
| A. | ($\frac{π}{3}$,$\frac{π}{2}$) | B. | (0,$\frac{π}{3}$) | C. | ($\frac{π}{6}$,$\frac{π}{2}$) | D. | (0,$\frac{π}{6}$) |
13.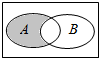 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )| A. | {2,3,4} | B. | {2,3,4,5} | C. | {3,4} | D. | {3,4,5} |
17.设命题p:?n∈N,n2>2n,则¬p为( )
| A. | ?n∈N,n2≤2n | B. | ?n∈N,n2<2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2<2n |
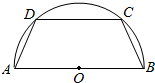 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.