题目内容
7. 如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,
如图所示的三角形数阵叫“牛顿调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数的和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则(1)第6行第2个数(从左往右数)为$\frac{1}{30}$;
(2)第n行第3个数(从左往右数)为$\frac{2}{n(n-1)(n-2)}$.
分析 根据“牛顿调和三角形”的特征,每个数是它下一个行左右相邻两数的和,得出将杨晖三角形中的每一个数Cnr都换成分数$\frac{1}{(n+1){C}_{n}^{r}}$,就得到一个莱布尼兹三角形,从而可求出第n(n≥3)行第3个数字,第6行第2个数.
解答 解:将杨晖三角形中的每一个数Cnr都换成分数$\frac{1}{(n+1){C}_{n}^{r}}$,
就得到牛顿调和三角形.
∵杨晖三角形中第n(n≥3)行第3个数字是Cn-12,
则“莱布尼兹调和三角形”第n(n≥3)行第3个数字是$\frac{1}{n{C}_{n-1}^{2}}$=$\frac{2}{n(n-1)(n-2)}$,
第6行第2个数$\frac{1}{6×5}$=$\frac{1}{30}$,
故答案为:$\frac{1}{30},\frac{2}{n(n-1)(n-2)}$
点评 本题考查归纳推理,解题的关键是通过观察分析归纳各数的关系,考查学生的观察分析和归纳能力,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.设m,n∈(0,+∞),若直线(m+2)x+(n+2)y-4=0与圆(x-1)2+(y-1)2=1相切,则m+n的最小值是( )
| A. | 4+4$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 4+$\sqrt{2}$ | D. | 4+2$\sqrt{2}$ |
19.已知函数f(x)=lnx+2sinα(α∈(0,$\frac{π}{2}$))的导函数f′(x),若存在x0<1使得f′(x0)=f(x0)成立,则实数α的取值范围为( )
| A. | ($\frac{π}{3}$,$\frac{π}{2}$) | B. | (0,$\frac{π}{3}$) | C. | ($\frac{π}{6}$,$\frac{π}{2}$) | D. | (0,$\frac{π}{6}$) |
17.设命题p:?n∈N,n2>2n,则¬p为( )
| A. | ?n∈N,n2≤2n | B. | ?n∈N,n2<2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2<2n |

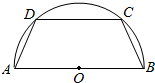 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.