题目内容
12.极坐标系中与圆ρ=6sinθ相切的一条直线的方程为( )| A. | ρsinθ=3 | B. | ρcosθ=3 | C. | $ρ=6sin(θ+\frac{π}{3})$ | D. | $ρ=6sin(θ-\frac{π}{3})$ |
分析 把直线与圆的极坐标方程分别化为直角坐标方程,利用直线与圆的相切的充要条件即可判断出结论.
解答 解:圆ρ=6sinθ,即:ρ2=6ρsinθ,化为直角坐标方程:x2+y2=6y,配方为x2+(y-3)2=9,圆心为(0,3),半径r=3.
对于B:直线ρcosθ=3化为x=3,圆心到此直线的距离d=3=r,
因此直线与圆相切,
故选:B.
点评 本题考查了极坐标方程与直角坐标方程的互化、点的直线的距离公式、直线与圆相切的充要条件,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
3.已知向量$\overrightarrow a$=(x,1),$\overrightarrow b$=(1,-1),若$\overrightarrow a$∥$\overrightarrow b$,则x=( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
20.若实数a>1,则函数f(x)=loga(x2-5x+6)的单调减区间为( )
| A. | ($\frac{5}{2}$,+∞) | B. | (3,+∞) | C. | (-∞,$\frac{5}{2}$) | D. | (-∞,2) |
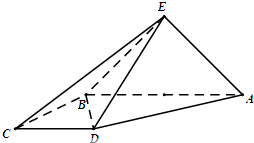 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.