题目内容
1.证明:(1)$\sqrt{3}-\sqrt{2}$>$\sqrt{5}-\sqrt{4}$
(2)$\sqrt{n+2}-\sqrt{n+1}$<$\sqrt{n+1}-\sqrt{n}$.
分析 使用分析法寻找使不等式成立的条件,只需条件恒成立即可;
解答 证明:(1)欲证$\sqrt{3}-\sqrt{2}$>$\sqrt{5}$-$\sqrt{4}$,
只需证($\sqrt{3}-\sqrt{2}$)2>($\sqrt{5}$-$\sqrt{4}$)2,即证5-2$\sqrt{6}$>9-4$\sqrt{5}$,
即证$\sqrt{6}$>2($\sqrt{5}$-1),
只需证6>4(6-2$\sqrt{5}$),即证9>4$\sqrt{5}$,
只需证81>80,
显然81>80恒成立,
∴$\sqrt{3}-\sqrt{2}$>$\sqrt{5}$-$\sqrt{4}$.
(2)欲证$\sqrt{n+2}-\sqrt{n+1}$<$\sqrt{n+1}-\sqrt{n}$,
只需证($\sqrt{n+2}-\sqrt{n+1}$)2<($\sqrt{n+1}-\sqrt{n}$)2,即证1-$\sqrt{(n+2)(n+1)}$<-$\sqrt{n(n+1)}$,
只需证$\sqrt{(n+2)(n+1)}$>$\sqrt{n(n+1)}$+1
只需证(n+2)(n+1)>n(n+1)+1+2$\sqrt{n(n+1)}$,
即证n+1>$\sqrt{n(n+1)}$,
只需证(n+1)2>n(n+1),即证n+1>n,
只需证1>0,
显然1>0恒成立,
∴$\sqrt{n+2}-\sqrt{n+1}$<$\sqrt{n+1}-\sqrt{n}$.
点评 本题考查了不等式的证明方法,属于中档题.

练习册系列答案
相关题目
11.若a∈R,则“a>3”是“a2-9>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.极坐标系中与圆ρ=6sinθ相切的一条直线的方程为( )
| A. | ρsinθ=3 | B. | ρcosθ=3 | C. | $ρ=6sin(θ+\frac{π}{3})$ | D. | $ρ=6sin(θ-\frac{π}{3})$ |
16.将曲线C按照伸缩变换$\left\{{\begin{array}{l}{x'=2x}\\{y'=3y}\end{array}}\right.$后得到的曲线方程为x'-y'+4=0,则曲线C的方程为( )
| A. | 2x+3y-4=0 | B. | 3x-2y+4=0 | C. | 2x-3y+4=0 | D. | 3x-2y+24=0 |




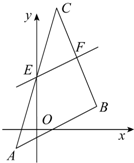 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求: