题目内容
4.已知函数f(x)=$\frac{{{x^2}-4x+5}}{x}$(x>0),当且仅当x=$\sqrt{5}$时,f(x)取到最小值为2$\sqrt{5}$-4.分析 f(x)=x+$\frac{5}{x}$-4,使用基本不等式求出f(x)的最小值即可.
解答 解:∵x>0,
∴f(x)=$\frac{{x}^{2}-4x+5}{x}$=x+$\frac{5}{x}$-4$≥2\sqrt{5}$-4.
当且仅当x=$\frac{5}{x}$即x=$\sqrt{5}$时取等号,
∴当x=$\sqrt{5}$时,f(x)取得最小值2$\sqrt{5}$-4.
故答案为:$\sqrt{5}$,2$\sqrt{5}$-4.
点评 本题考查了函数最值的求法,基本不等式的应用,也可利用函数的单调性来解决.属于中档题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
14.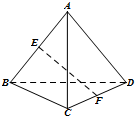 如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
 如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
12.极坐标系中与圆ρ=6sinθ相切的一条直线的方程为( )
| A. | ρsinθ=3 | B. | ρcosθ=3 | C. | $ρ=6sin(θ+\frac{π}{3})$ | D. | $ρ=6sin(θ-\frac{π}{3})$ |
16.将曲线C按照伸缩变换$\left\{{\begin{array}{l}{x'=2x}\\{y'=3y}\end{array}}\right.$后得到的曲线方程为x'-y'+4=0,则曲线C的方程为( )
| A. | 2x+3y-4=0 | B. | 3x-2y+4=0 | C. | 2x-3y+4=0 | D. | 3x-2y+24=0 |




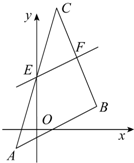 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,△CEF的面积是△CAB面积的$\frac{1}{4}$.求: