题目内容
已知f（x）=
，则f[f（-1）]=（ ）
|
| A、π-1 | B、0 | C、1 | D、π |
考点：函数的值
专题：函数的性质及应用
分析：利用分段函数的性质求解．
解答：
解：∵函数f（x）=
，
∴f（-1）=0，
f[f（-1）]=f（0）=0．
故选：B．
|
∴f（-1）=0，
f[f（-1）]=f（0）=0．
故选：B．
点评：本题考查函数值的求法，解题时要认真审题，注意分段函数的性质的灵活运用．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
在三角形ABC中，acosB=bcosA，则三角形ABC是（ ）
| A、钝角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等边三角形 |
下列各组中两个函数是同一函数的是（ ）
A、f(x)=
| ||
| B、f（r）=πr2（r≥0）与g（x）=πx2（x≥0） | ||
| C、f(x)=logaax(a＞0，且a≠1）与g(x)=alogax(a＞0，且a≠1) | ||
D、f(x)=|x|与g(t)=(
|
用反证法证明命题：“已知a、b为实数，若a＞0，b＜0，则方程x2+ax+b=0?至少有一个实根”时，要做的假设是（ ）
| A、方程x2+ax+b=0没有实根 |
| B、方程x2+ax+b=0至多有一个实根 |
| C、方程x2+ax+b=0至多有两个实根 |
| D、方程x2+ax+b=0恰好有两个实根 |
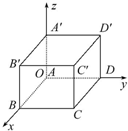如图，已知长方体ABCD-A′B′C′D的边长为AB=12，AD=8，AA′=5．以这个长方体的顶点A为坐标原点，射线AB，AD，AA′分别为x轴、y轴、z轴的正半轴，建立空间直角坐标系，