题目内容
设f(x)=|lnx|,若函数g(x)=f(x)-ax在区间(0,5]上有三个零点,则实数a的取值范围是 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:首先,画出函数f(x)=|lnx|的图象,然后,借助于图象,结合在区间(0,5]上有三个零点,进行判断.
解答:
解:解:函数f(x)=|lnx|的图象如图示:
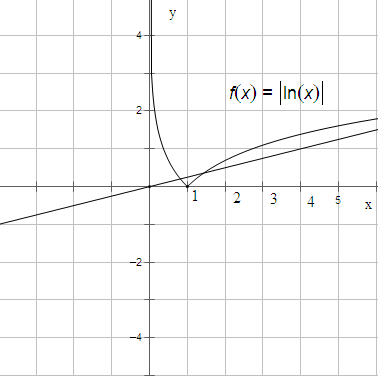
当a≤0时,显然,不合乎题意,
当a>0时,如图示,
当x∈(0,1]时,存在一个零点,
当x>1时,f(x)=lnx,
可得g(x)=lnx-ax,(x∈(1,5])
g′(x)=
-a=
,
若g′(x)<0,可得x>
,g(x)为减函数,
若g′(x)>0,可得x<
,g(x)为增函数,
此时f(x)必须在[1,5]上有两个交点,
∴
,解得,
≤a<
,
故答案为:[
,
).
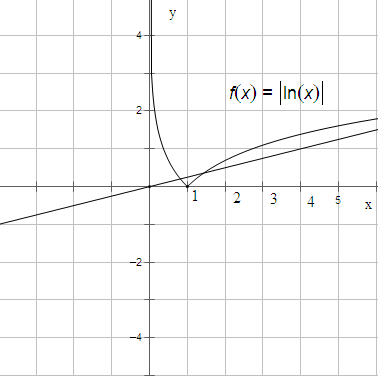
当a≤0时,显然,不合乎题意,
当a>0时,如图示,
当x∈(0,1]时,存在一个零点,
当x>1时,f(x)=lnx,
可得g(x)=lnx-ax,(x∈(1,5])
g′(x)=
| 1 |
| x |
| 1-ax |
| x |
若g′(x)<0,可得x>
| 1 |
| a |
若g′(x)>0,可得x<
| 1 |
| a |
此时f(x)必须在[1,5]上有两个交点,
∴
|
| ln5 |
| 5 |
| 1 |
| e |
故答案为:[
| ln5 |
| 5 |
| 1 |
| e |
点评:本题重点考查函数的零点,属于中档题,难度中等.

练习册系列答案
相关题目
在各项都为正数的等比数列{an}中,首项为3,前3项和为21,则q等于( )
| A、6 | B、3 | C、2 | D、1 |