题目内容
已知tanα=
,α是第三象限角,则cosα= .
| 3 |
| 4 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式两边平方,利用同角三角函数间基本关系化简求出sin2α的值,根据α为第三象限角求出sinα的值,进而求出cosα的值.
解答:
解:∵tanα=
,
∴tan2α=
=
,
∴
=
,
解得:sin2α=
,
又∵α是第三象限角,
∴sinα=-
,
∴cosα=-
=-
=-
.
故答案为:-
| 3 |
| 4 |
∴tan2α=
| sin2α |
| cos2α |
| 9 |
| 16 |
∴
| sin2α |
| 1-sin2α |
| 9 |
| 16 |
解得:sin2α=
| 9 |
| 25 |
又∵α是第三象限角,
∴sinα=-
| 3 |
| 5 |
∴cosα=-
| 1-sin2α |
1-(-
|
| 4 |
| 5 |
故答案为:-
| 4 |
| 5 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
在△ABC中,已知a=
,b=1,A=45°,则B等于( )
| 2 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
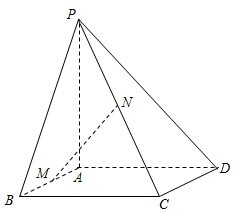 如图,在四棱锥中,底面ABCD为矩形,PA⊥底面ABCD,M、N分别是AB、PC中点.
如图,在四棱锥中,底面ABCD为矩形,PA⊥底面ABCD,M、N分别是AB、PC中点.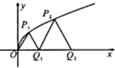 如图,抛物线y=
如图,抛物线y=