题目内容
定积分∫
sinxdx= .
2π π |
考点:定积分
专题:计算题,导数的综合应用
分析:求出被积函数的导函数,分别代入积分上限和积分下限后作差得答案.
解答:
解:∫
sinxdx=-cosx
=-cos2π+cosπ=-2.
故答案为:-2.
2π π |
| | | 2π π |
故答案为:-2.
点评:本题考查了定积分,关键是求出被积函数的原函数,是基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
若数列{an}满足
-
=d(n∈N*,d为常数),则称数列{an}为“调和数列”,已知正项数列{
}为“调和数列”,且b1+b2+…+b11=110,则b5•b7的最大值是( )
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| bn |
| A、10 | B、100 |
| C、110 | D、200 |
在△ABC中,a、b、c分别为角A,B,C所对的边,且b2+c2-a2=
bc,则A等于( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
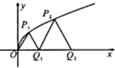 如图,抛物线y=
如图,抛物线y=