题目内容
7.已知a∈{0,1,2},b∈{-1,1,3,5},则函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率是( )| A. | $\frac{5}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 先求出基本事件总数n=3×4=12,再求出函数f(x)=ax2-2bx在区间(1,+∞)上为增函数满足条件的基本事件个数,由此能求出函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率.
解答 解:∵a∈{0,1,2},b∈{-1,1,3,5},
∴基本事件总数n=3×4=12,
函数f(x)=ax2-2bx在区间(1,+∞)上为增函数,
①当a=0时,f(x)=-2bx,符合条件的只有:(0,-1),即a=0,b=-1;
②当a≠0时,需要满足$\frac{b}{a}≤1$,符合条件的有:(1,-1),(1,1),(2,-1),(2,1),共4种,
∴函数f(x)=ax2-2bx在区间(1,+∞)上为增函数的概率是p=$\frac{5}{12}$.
故选:A.
点评 本题考查概率的求不地,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
17.一抛物线形拱桥,当水面宽4米时,水面离拱顶2米,若水面下降1米,则水面的宽为( )
| A. | $\sqrt{6}$米 | B. | 2$\sqrt{6}$米 | C. | 6米 | D. | 8米 |
15.将函数$y=2sin(2x+\frac{π}{6})$的图象向右平移$\frac{1}{4}$个周期后,所得图象对应的函数为f(x),则函数f(x)的单
调递增区间( )
调递增区间( )
| A. | $[kπ-\frac{π}{12},kπ+\frac{5π}{12}](k∈Z)$ | B. | $[kπ+\frac{5π}{12},kπ+\frac{11π}{12}](k∈Z)$ | ||
| C. | $[kπ-\frac{5π}{24},kπ+\frac{7π}{24}](k∈Z)$ | D. | $[kπ+\frac{7π}{24},kπ+\frac{19π}{24}](k∈Z)$ |
19.实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x-y-1≤0\\ x-2y+1≥0\end{array}\right.$,则2x-y的最大值为( )
| A. | $-\frac{1}{2}$ | B. | 0 | C. | 2 | D. | 4 |
16.对于命题p:?x∈R,使得x2+x+1<0,则¬p是( )
| A. | ¬p:?x∈R,x2+x+1>0 | B. | ¬p:?x∈R,x2+x+1≠0 | ||
| C. | ¬p:?x∈R,x2+x+1≥0 | D. | ¬p:?x∈R,x2+x+1<0 |
17.已知A,B,C三点在球O的球面上,AB=BC=CA=3,且球心O到平面ABC的距离等于球半径的$\frac{1}{3}$,则球O的表面积为( )
| A. | 36π | B. | 4π | C. | $\frac{27}{4}$π | D. | $\frac{27}{2}$π |
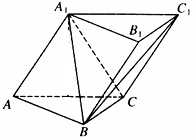 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,