题目内容
7.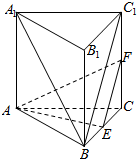 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面ABC等边三角形,E,F分别是BC,CC1的中点.求证:(Ⅰ) EF∥平面A1BC1;
(Ⅱ) 平面AEF⊥平面BCC1B1.
分析 (Ⅰ)由三角形中位线定理得EF∥BC1,由此能证明EF∥平面A1BC1.
(Ⅱ)由三棱柱ABC-A1B1C1是直三棱柱,得AE⊥BB1,由正三角形性质得AE⊥BC,由此能证明平面AEF⊥平面BCC1B1.
解答  证明:(Ⅰ)因为E,F分别是BC,CC1的中点,
证明:(Ⅰ)因为E,F分别是BC,CC1的中点,
所以EF∥BC1.
又因为BC1?平面A1BC1,EF?平面A1BC1,
所以EF∥平面A1BC1.(6分)
(Ⅱ)因为三棱柱ABC-A1B1C1是直三棱柱,
所以BB1⊥平面ABC.又AE?平面ABC,
所以AE⊥BB1.
又因为△ABC为正三角形,E为BC的中点,
所以AE⊥BC.
又BB1∩BC=B,所以AE⊥平面BCC1B1.
又AE?平面AEF,所以平面AEF⊥平面BCC1B1.(12分)
点评 本题考查线面平行的证明,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
17.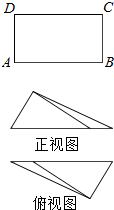 如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
 如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\sqrt{3}$,BC=1,沿AC将矩形ABCD折叠,连接BD,所得三棱锥D-ABC的正视图和俯视图如图所示,则三棱锥D-ABC的侧视图的面积为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
18.已知O为坐标原点,直线y=2与x2+y2+Dx-4y=0交于两点M,N,则∠MON=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15.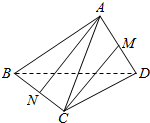 如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值为( )
如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值为( )
 如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值为( )
如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值为( )| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{8}$ | D. | $-\frac{7}{8}$ |
2.已知命题p:函数f(x)=x2-2mx+4在[2,+∞)上单调递增;命题q:关于x的不等式mx2+2(m-2)x+1>0对任意x∈R恒成立.若p∨q为真命题,p∧q为假命题,则实数m的取值范围为( )
| A. | (1,4) | B. | [-2,4] | C. | (-∞,1]∪(2,4) | D. | (-∞,1)∪(2,4) |
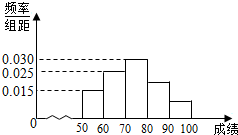 某校共有400名学生参加了一次数学竞赛,竞赛成绩都在[50,100]内,且频率分布直方图如图所示(成绩分组为[50,60],[60,70],[70,80),[80,90),[90,100]),则在本次竞赛中,得分不低于80分的人数为120.
某校共有400名学生参加了一次数学竞赛,竞赛成绩都在[50,100]内,且频率分布直方图如图所示(成绩分组为[50,60],[60,70],[70,80),[80,90),[90,100]),则在本次竞赛中,得分不低于80分的人数为120.