题目内容
实数x,y满足不等式
,则ω=
的取值范围是( )
|
| y+1 |
| x+1 |
A、[-1,
| ||
B、[-1,
| ||
C、(-∞,-1]∪[
| ||
D、(-∞,-1)∪(
|
考点:简单线性规划
专题:数形结合
分析:由约束条件作差可行域,然后结合ω=
的几何意义及直线x+y=3与x-2y-2=0的斜率得答案.
| y+1 |
| x+1 |
解答:
解由约束条件
作出可行域如图,

则ω=
的几何意义为可行域内的动点与定点(-1,-1)连线的斜率,
由图可知,ω=
的取值范围是(-∞,-1)∪(
,+∞).
故选:D.
|

则ω=
| y+1 |
| x+1 |
由图可知,ω=
| y+1 |
| x+1 |
| 1 |
| 2 |
故选:D.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
由二项式定理知识可将[(x+y)n-(x-y)n](n∈N*)展开并化简.若a=
(
)dx,则在(a+5)2n+1(n∈N*)的小数表示中,小数点后面至少连续有零的个数是( )
| ∫ | 26 0 |
| 1 | ||
2
|
| A、2n-1 | B、2n |
| C、2n+1 | D、2n+2 |
下列函数中,满足f(xy)=f(x)+f(y)的单调递增函数是( )
| A、f(x)=log2x | ||
| B、f(x)=x2 | ||
| C、f(x)=2x | ||
D、f(x)=log
|
在平面直角坐标系中,定义两点P(x1,y1)与Q(x2,y2)之间的“直角距离”为d(P,Q)=|x1-x2|+|y1-y2|.给出下列命题:
(1)若P(1,2),Q(sinα,cosα)(α∈R),则d(P,Q)的最大值为3-
;
(2)若P,Q是圆x2+y2=1上的任意两点,则d(P,Q)的最大值为2
;
(3)若P(1,3),点Q为直线y=2x上的动点,则d(P,Q)的最小值为
.
其中为真命题的是( )
(1)若P(1,2),Q(sinα,cosα)(α∈R),则d(P,Q)的最大值为3-
| 2 |
(2)若P,Q是圆x2+y2=1上的任意两点,则d(P,Q)的最大值为2
| 2 |
(3)若P(1,3),点Q为直线y=2x上的动点,则d(P,Q)的最小值为
| 1 |
| 2 |
其中为真命题的是( )
| A、(1)(2)(3) |
| B、(2) |
| C、(3) |
| D、(2)(3) |
已知由长方体截去一个棱锥所得几何体的三视图如图所示,则该几何体的体积为( )


| A、16 | ||
B、
| ||
C、
| ||
D、
|
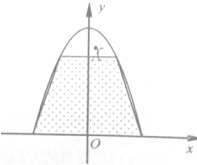 如图,有一块钢板其边缘由一条线段及一段抛物线弧组成,其中抛物线弧的方程为y=-2x2+2(-1≤x≤1).计划将此钢板切割成等腰梯形,切割时以边缘的一条线段为梯形的下底.
如图,有一块钢板其边缘由一条线段及一段抛物线弧组成,其中抛物线弧的方程为y=-2x2+2(-1≤x≤1).计划将此钢板切割成等腰梯形,切割时以边缘的一条线段为梯形的下底.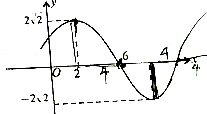 函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.
函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.