题目内容
已知抛物线E:y2=4x,点F(a,0),直线l:x=-a(a>0).
(Ⅰ)P为直线l上的点,R是线段PF与y轴的交点,且点Q满足RQ⊥FP,PQ⊥l.当a=1时,试问点Q是否在抛物线E上,并说明理由;
(Ⅱ)过点F的直线交抛物线E于A,B两点,直线OA,OB分别与直线l交于M,N两点(O为坐标原点),求证:以MN为直径的圆恒过定点,并求出定点坐标.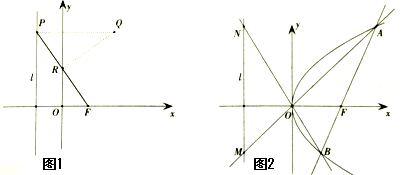
(Ⅰ)P为直线l上的点,R是线段PF与y轴的交点,且点Q满足RQ⊥FP,PQ⊥l.当a=1时,试问点Q是否在抛物线E上,并说明理由;
(Ⅱ)过点F的直线交抛物线E于A,B两点,直线OA,OB分别与直线l交于M,N两点(O为坐标原点),求证:以MN为直径的圆恒过定点,并求出定点坐标.

考点:直线与圆锥曲线的关系
专题:数形结合,方程思想,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据题意,结合图形,利用抛物线的定义,得出Q点在抛物线E;
(Ⅱ)由图形的对称性得出定点在x轴上,设出定点的坐标,讨论①直线AB的斜率不存在时与②直线AB的斜率存在时,求出以MN为直径的圆恒过定点是什么.
(Ⅱ)由图形的对称性得出定点在x轴上,设出定点的坐标,讨论①直线AB的斜率不存在时与②直线AB的斜率存在时,求出以MN为直径的圆恒过定点是什么.
解答:
解:(Ⅰ)由已知a=1,得F(1,0)为焦点,直线l:x=-1为准线;
∵O点为FC的中点,且OR∥PC,∴点R是线段PF的中点,
又∵RQ⊥PF,∴QR是PF的垂直平分线,∴PQ=QF;
根据抛物线的定义知,Q点在抛物线E:y2=4x上;
(Ⅱ)由图形的对称性知,定点在x轴上,设定点坐标为K(m,0),
①当直线AB的斜率不存在时,设直线AB方程为x=a,
求得A(a,2
),B(a,-2
),M(-a,2
),N(-a,-2
);
显然,以MN为直径的圆恒过定点(2
-a,0),(-2
-a,0);
②当直线AB的斜率存在时,设直线AB的方程为y=k(x-a),代入y2=4x得k2x2-(2ak2+4)x+a2k2=0;
设A(x1,2
),B(x2,-2
),
由根与系数的关系得,x1+x2=
,x1x2=a2;
又kOA=
kOB=-
∴直线OA的方程为y=
x,
直线OB的方程为y=-
x;
∴M(-a,-
),N(-a,
);
由于圆恒过点Km0),根据圆的性质得∠MKN=90°,
即
•
=0,
∴
=(-a-m,-
),
=(-a-m,
),
代入上式向量的数量积,得;(a+m)2-
=0,
∴(a+m)2-4a=0,解得m=±2
-a;
∴以MN为直径的圆恒过定点(2
-a,0),(-2
-a,0).
∵O点为FC的中点,且OR∥PC,∴点R是线段PF的中点,
又∵RQ⊥PF,∴QR是PF的垂直平分线,∴PQ=QF;
根据抛物线的定义知,Q点在抛物线E:y2=4x上;
(Ⅱ)由图形的对称性知,定点在x轴上,设定点坐标为K(m,0),
①当直线AB的斜率不存在时,设直线AB方程为x=a,
求得A(a,2
| a |
| a |
| a |
| a |
显然,以MN为直径的圆恒过定点(2
| a |
| a |
②当直线AB的斜率存在时,设直线AB的方程为y=k(x-a),代入y2=4x得k2x2-(2ak2+4)x+a2k2=0;
设A(x1,2
| x1 |
| x2 |
由根与系数的关系得,x1+x2=
| 2ak2+4 |
| k2 |
又kOA=
| 2 | ||
|
| 2 | ||
|
∴直线OA的方程为y=
| 2 | ||
|
直线OB的方程为y=-
| 2 | ||
|
∴M(-a,-
| 2a | ||
|
| 2a | ||
|
由于圆恒过点Km0),根据圆的性质得∠MKN=90°,
即
| KM |
| KN |
∴
| KM |
| 2a | ||
|
| KN |
| 2a | ||
|
代入上式向量的数量积,得;(a+m)2-
| 4a2 | ||
|
∴(a+m)2-4a=0,解得m=±2
| a |
∴以MN为直径的圆恒过定点(2
| a |
| a |
点评:本题考查了抛物线的定义域几何性质的应用问题,也考查了直线方程、圆的方程的应用问题,考查了用代数的方法研究圆锥曲线的性质的问题,考查了数形结合的思想与方程的思想,是综合性题目.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知函数f(x)=
且f(m)=
,则m的值为( )
|
| 5 |
| 4 |
A、log2
| ||
B、
| ||
C、-
| ||
D、±
|
已知直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=4相交于A,B两点,且△ABC为等边三角形,则实数a=( )
A、±
| ||||
B、±
| ||||
| C、1或7 | ||||
D、4±
|
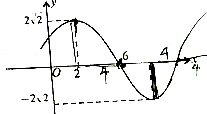 函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.
函数y=Asin(ωx+ϕ)(其中A>0,ω>0,0<ϕ<π)的图象的一部分如图所示.