题目内容
17.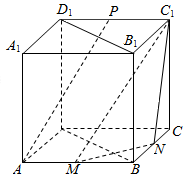 如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点.求证:(1)AP∥平面C1MN;
(2)平面B1BDD1⊥平面C1MN.
分析 (1)推导出四边形AMC1P为平行四边形,从而AP∥C1M,由此能证明AP∥平面C1MN.
(2)连结AC,推导出MN⊥BD,DD1⊥MN,从而MN⊥平面BDD1B1,由此能证明平面B1BDD1⊥平面C1MN.
解答  证明:(1)在正方体ABCD-A1B1C1D1中
证明:(1)在正方体ABCD-A1B1C1D1中
∵M,N,P分别为棱AB,BC,C1D1的中点,
∴AM=PC1,
又AM∥CD,PC1∥CD,故AM∥PC1,
∴四边形AMC1P为平行四边形,
∴AP∥C1M,
又AP?平面C1MN,C1M?平面C1MN,
∴AP∥平面C1MN.
(2)连结AC,在正方形ABCD中,AC⊥BD,
又M、N分别为棱AB、BC的中点,∴MN∥AC,
∴MN⊥BD,
在正方体ABCD-A1B1C1D1中,DD1⊥平面ABCD,
又MN?平面ABCD,∴DD1⊥MN,
而DD1∩DB=D,DD1、DB?平面BDD1B1,
∴MN⊥平面BDD1B1,
又MN?平面C1MN,∴平面B1BDD1⊥平面C1MN.
点评 本题考查线面平行的证明,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.已知e为自然对数的底数,若对任意的x∈[0,1],总存在唯一的y∈[-1,1],使得x+y2ey-a=0成立,则实数a的取值范围是( )
| A. | [1,e] | B. | $(1+\frac{1}{e},e]$ | C. | (1,e] | D. | $[1+\frac{1}{e},e]$ |
2.我国数学史上有一部堪与欧几里得《几何原本》媲美的书,这就是历来被尊为算经之首的《九章算术》,其中卷第五《商功》有一道关于圆柱体的体积试题:今有圆堡,周四丈八尺,高一丈一尺,问积几何?其意思是:含有圆柱形的土筑小城堡,底面周长是4丈8尺,高1丈1尺,问它的体积是多少?若π取3,估算小城堡的体积为( )
| A. | 1998立方尺 | B. | 2012立方尺 | C. | 2112立方尺 | D. | 2324立方尺 |
9.若$\overrightarrow b=(sin{75°},cos{105°})$,$|\overrightarrow a|=3|\overrightarrow b|$,且$(\sqrt{3}\overrightarrow a+\overrightarrow b)•\overrightarrow b=-2$,则 $cos<\overrightarrow a,\overrightarrow b>$=( )
| A. | $-\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |