题目内容
7.已知P={x|x2-8x-20≤0},S={x|1-m≤x≤1+m},是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的范围;若不存在,请说明理由.分析 求出集合P的等价条件,根据充分条件和必要条件的定义建立方程关系进行求解即可.
解答 解:P={x|x2-8x-20≤0}={x|-2≤x≤10},
若存在实数m,使x∈P是x∈S的充要条件,
则$\left\{\begin{array}{l}{1+m≥1-m}\\{1+m=10}\\{1-m=-2}\end{array}\right.$,即$\left\{\begin{array}{l}{m≥0}\\{m=9}\\{m=3}\end{array}\right.$,此时m无解,
即不存在实数m,使x∈P是x∈S的充要条件.
点评 本题主要考查充分条件和必要条件的应用,求出集合的等价条件,建立不等式关系是解决本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
15.已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,点A是椭圆M与圆C:x2+(y-2$\sqrt{2}$b)2=$\frac{4}{9}$m2在第一象限的交点,且点A到F2的距离等于$\frac{1}{3}$m,若椭圆M上一动点到点F1与到点C的距离之差的最大值为2a-m,则椭圆M的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的最小值为-2,且对于任意x∈R,恒有f(x+$\frac{π}{2}$)+f(x)=0,又f(0)=1,则函数f(x)在区间[0,π]上的增区间为( )
| A. | [0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,$\frac{2π}{3}$] | C. | [0,$\frac{π}{6}$]∪[$\frac{2π}{3}$,π] | D. | [0,$\frac{π}{6}$]和[$\frac{2π}{3}$,π] |
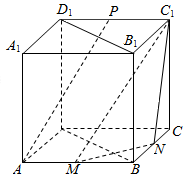 如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点. 如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和棱CC1的中点.求证:EB1∥DF,ED∥B1F.(提示:设G是DD1的中点,分别连接EG,GC1)
如图所示,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和棱CC1的中点.求证:EB1∥DF,ED∥B1F.(提示:设G是DD1的中点,分别连接EG,GC1)