题目内容
8.已知e为自然对数的底数,若对任意的x∈[0,1],总存在唯一的y∈[-1,1],使得x+y2ey-a=0成立,则实数a的取值范围是( )| A. | [1,e] | B. | $(1+\frac{1}{e},e]$ | C. | (1,e] | D. | $[1+\frac{1}{e},e]$ |
分析 由x+y2ey-a=0成立,解得y2ey=a-x,根据题意可得:a-1≥(-1)2e-1,且a-0≤12×e1,解出并且验证等号是否成立即可得出.
解答 解:由x+y2ey-a=0成立,解得y2ey=a-x,
∴对任意的x∈[0,1],总存在唯一的y∈[-1,1],使得x+y2ey-a=0成立,
∴a-1≥(-1)2e-1,且a-0≤12×e1,
解得$1+\frac{1}{e}$≤a≤e,其中a=1+$\frac{1}{e}$时,y存在两个不同的实数,因此舍去,a的取值范围是$(1+\frac{1}{e},e]$.
故选:B.
点评 本题考查了函数的单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13.已知集合M={x|x<0},N={x|x2-x-2<0},则M∩N=( )
| A. | {x|-1<x<0} | B. | {x|-2<x<0} | C. | {x|x<2} | D. | {x|x<1} |
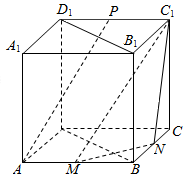 如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,M,N,P分别为棱AB,BC,C1D1的中点.