题目内容
已知圆C:x2+y2=1,点P(x0,y0)是直线l:3x+2y-4=0上的动点,若在圆C上总存在不同的两点A,B使得
+
=
,则x0的取值范围是 .
| OA |
| OB |
| OP |
考点:向量的加法及其几何意义
专题:平面向量及应用
分析:在圆C上总存在不同的两点A,B使得
+
=
,可知:四边形OAPB是菱形,于是AB垂直平分OP.分类讨论:当直线AB的斜率为0时,此时在⊙C上不存在不同的两点A,B满足条件.
当直线AB的斜率不存在时,可得P(
,0),此时直线AB为:x=
,满足条件.
当直线AB的斜率存在且不为0时,利用AB⊥OP,kOP=
,可得直线AB方程为2x0x+2y0y-
-
=0,
圆心到直线AB的距离d=
<1,即
+
<4,再利用3x0+2y0-4=0,即可解出.
| OA |
| OB |
| OP |
当直线AB的斜率不存在时,可得P(
| 4 |
| 3 |
| 2 |
| 3 |
当直线AB的斜率存在且不为0时,利用AB⊥OP,kOP=
| y0 |
| x0 |
| x | 2 0 |
| y | 2 0 |
圆心到直线AB的距离d=
| ||||||
| 2 |
| x | 2 0 |
| y | 2 0 |
解答:
解:∵在圆C上总存在不同的两点A,B使得
+
=
,
∴四边形OAPB是菱形,∴AB垂直平分OP.
当直线AB的斜率为0时,由直线l:3x+2y-4=0得P(0,2),此时在⊙C上不存在不同的两点A,B满足条件.
当直线AB的斜率不存在时,由直线l:3x+2y-4=0可得P(
,0),此时直线AB为:x=
,满足条件.
当直线AB的斜率存在且不为0时,
∵AB⊥OP,kOP=
,∴kAB=-
.
∴直线AB方程为y-
=-
(x-
),化为2x0x+2y0y-
-
=0,
圆心到直线AB的距离d=
<1,即
+
<4,
又3x0+2y0-4=0,化为13
-24x0<0,
解得0<x0<
,
∴x0的取值范围是(0,
).
故答案为:(0,
).
| OA |
| OB |
| OP |
∴四边形OAPB是菱形,∴AB垂直平分OP.
当直线AB的斜率为0时,由直线l:3x+2y-4=0得P(0,2),此时在⊙C上不存在不同的两点A,B满足条件.
当直线AB的斜率不存在时,由直线l:3x+2y-4=0可得P(
| 4 |
| 3 |
| 2 |
| 3 |
当直线AB的斜率存在且不为0时,
∵AB⊥OP,kOP=
| y0 |
| x0 |
| x0 |
| y0 |
∴直线AB方程为y-
| y0 |
| 2 |
| x0 |
| y0 |
| x0 |
| 2 |
| x | 2 0 |
| y | 2 0 |
圆心到直线AB的距离d=
| ||||||
| 2 |
| x | 2 0 |
| y | 2 0 |
又3x0+2y0-4=0,化为13
| x | 2 0 |
解得0<x0<
| 24 |
| 13 |
∴x0的取值范围是(0,
| 24 |
| 13 |
故答案为:(0,
| 24 |
| 13 |
点评:本题考查了菱形的性质、向量的平行四边形法则、相互垂直的直线斜率之间的关系、点到直线的距离公式、直线与圆的位置关系等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
椭圆
(φ为参数)的长轴长为( )
|
| A、3 | B、5 | C、6 | D、10 |
直线l与圆x2+y2+2x-4y+1=0相交于A,B两点,若弦AB的中点(-2,3),则直线l的方程为( )
| A、x+y-3=0 |
| B、x+y-1=0 |
| C、x-y+5=0 |
| D、x-y-5=0 |
函数f(x)=sinx+
在区间[0,+∞)内( )
| x |
| A、没有零点 |
| B、有且仅有1个零点 |
| C、有且仅有2个零点 |
| D、有且仅有3个零点 |
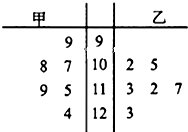 在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的6次培训成绩如茎叶图所示: