题目内容
17.设等比数列{an}的前n项和为Sn,若a3=4,S3=7,则S6的值为( )| A. | 31 | B. | 32 | C. | 63或$\frac{133}{27}$ | D. | 64 |
分析 设等比数列{an}的公比为q,由a3=4,S3=7,可得${a}_{1}{q}^{2}$=4,${a}_{1}(1+q+{q}^{2})$=7,解得a1,q.再利用等比数列的求和公式即可得出.
解答 解:设等比数列{an}的公比为q,∵a3=4,S3=7,
∴${a}_{1}{q}^{2}$=4,${a}_{1}(1+q+{q}^{2})$=7,
解得a1=1,q=2,或q=$-\frac{2}{3}$,a1=9.
当a1=1,q=2时,则S6=$\frac{{2}^{6}-1}{2-1}$=63.
当q=$-\frac{2}{3}$,a1=9时,S6=$\frac{9[1-(-\frac{2}{3})^{6}]}{1-(-\frac{2}{3})}$=$\frac{133}{27}$.
∴S6=63或$\frac{133}{27}$,
故选:C.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
7.在平面直角坐标系xOy中,以点(1,0)为圆心且与直线mx-y-2m-1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为( )
| A. | (x-1)2+y2=1 | B. | (x-1)2+y2=4 | C. | (x-1)2+y2=2 | D. | (x-1)2+y2=$\sqrt{2}$ |
2.命题p:?x0∈R,x0≤2的否定是( )
| A. | ¬p:?x∈R,x≤2 | B. | ¬p:?x∈R,x>2 | C. | ¬p:?x∈R,x>2 | D. | ¬p:?x∈R,x≤2 |
2.已知a=9${\;}^{\frac{1}{3}}$,b=3${\;}^{\frac{2}{5}}$,c=4${\;}^{\frac{1}{5}}$,则( )
| A. | b<a<c | B. | a>b>c | C. | a<b<c | D. | c<a<b |
19.定义运算a⊕b=$\left\{\begin{array}{l}a\begin{array}{l}{\;},{a<b}\end{array}\\ b\begin{array}{l}{\;},{a≥b}\end{array}\end{array}$若函数f(x)=2x⊕2-x,则f(x)的值域是( )
| A. | [1,+∞) | B. | (0,+∞) | C. | (0,1] | D. | $[{\frac{1}{2},1}]$ |
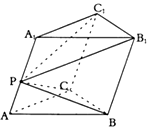 如图,P为三棱柱ABC-A1B1C1的侧棱AA1上的一个动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为$\frac{3}{2}V$(用V表示)
如图,P为三棱柱ABC-A1B1C1的侧棱AA1上的一个动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为$\frac{3}{2}V$(用V表示)