题目内容
已知两直线x+y-
=0与x+y+
=0所夹带形区域为D（包括边界），则点P（cosα，sinα）与D的关系是 ．
| 2 |
| 2 |
考点：直线和圆的方程的应用
专题：直线与圆
分析：作出平面区域D，利用D的轨迹，结合直线和圆的位置关系即可得到结论．
解答：
解：点P的轨迹为半径为1的圆x2+y2=1，
则圆心到直线x+y-
=0的距离d=
=1，
圆心到直线x+y+
=0的距离d=
=1，
则圆与两直线x+y-
=0与x+y+
=0都相切，
即点P（cosα，sinα）在区间D内，
即P∈D，
故答案为：P∈D，
解：点P的轨迹为半径为1的圆x2+y2=1，则圆心到直线x+y-
| 2 |
|-
| ||
|
圆心到直线x+y+
| 2 |
|
| ||
|
则圆与两直线x+y-
| 2 |
| 2 |
即点P（cosα，sinα）在区间D内，
即P∈D，
故答案为：P∈D，
点评：本题主要考查直线和圆的位置关系的应用，利用数形结合是解决本题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
已知向量
=（x-4，1），
=（x+5，y），x，y∈（0，+∞），且
∥
，则xy取最小值时y的值为（ ）
| a |
| b |
| a |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
| D、1 |
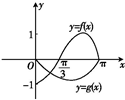已知y=f（x）是偶函数，y=g（x）是奇函数，它们的定义域均为[-π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式| f(x) |
| g(x) |
A、（-
| ||||||
B、（
| ||||||
C、（-
| ||||||
D、（-
|