题目内容
13.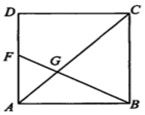 如图,在正方形 ABCD中,F是 AD 的中点,BF与 AC交于点 G,则△BGC 与四边形 CGFD的面积之比是4:5.
如图,在正方形 ABCD中,F是 AD 的中点,BF与 AC交于点 G,则△BGC 与四边形 CGFD的面积之比是4:5.
分析 设△AFG的面积为a,利用面积比等于相似比平方可得出△BGC的面积,$\frac{FG}{GB}=\frac{AF}{BC}=\frac{1}{2}$,可得出△ABG的面积,求出△ABC的面积即可得出△ADC的面积,也可得出四边形CGFD的面积,这样即可计算△BGC与四边形CGFD的面积之比.
解答 解:设△AFG的面积为a,
∵点F是AD中点,
∴AF=FD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∵AD∥BC,
∴△AFG∽△CBG,
∴$\frac{{S}_{△AFG}}{{S}_{△BCG}}$=$\frac{1}{4}$,
∴S△BCG=4a,
∵$\frac{FG}{GB}=\frac{AF}{BC}=\frac{1}{2}$,
∴$\frac{{S}_{△AFG}}{{S}_{△ABG}}$=$\frac{1}{2}$,
∴S△ABG=2a,
则S△ABC=S△BCG+S△ABG=S△ACD=6a,
∴S四边形CGFD=S△ACD-S△AFG=5a,
故S△BGC:S四边形CGFD=4a:5a=4:5.
故答案为4:5.
点评 本题考查了相似三角形的判定与性质,解答本题用到的知识点为:相似三角形的面积比等于相似比平方,②底边在一条直线上的且等高的三角形,面积之比等于底边之比.

练习册系列答案
相关题目
3.若直线l:ax+by=0与圆C:(x-2)2+(y+2)2=8相交,则直线l的倾斜角不等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{5π}{6}$ |
4.从长度分别位2、4、6、8、10的五条线段中,任取3条,则所得的3条线段中能组成三角形的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{10}$ |
8.已知数列{an}满足a1=2,an+1-an=-1(n∈N+),则此数列的通项an等于( )
| A. | n2+1 | B. | n+1 | C. | 1-n | D. | 3-n |
18.设$\frac{1}{2}$<($\frac{1}{2}$)b<($\frac{1}{2}$)a<1,那么( )
| A. | 1<aa<ab | B. | aa<ab<1 | C. | ab<aa<1 | D. | 1ab<aa |
2.$\root{4}{a-2}$+(a-4)0有意义,则a的取值范围是( )
| A. | a≥2 | B. | 2≤a<4或a>4 | C. | a≠2 | D. | a≠4 |