题目内容
3.函数f(x)=$\frac{1}{3}{x^3}+\frac{1}{2}m{x^2}$+x在R上有极值,则m的取值范围是{m|m>2或m<-2}.分析 求出函数的导数,解关于导函数的不等式,得到关于导函数的不等式有2个不相等的实数根,从而求出m的范围即可.
解答 解:f(x)=$\frac{1}{3}{x^3}+\frac{1}{2}m{x^2}$+x,
f′(x)=x2+mx+1
若f(x)在R上有极值,
则△=m2-4>0,
解得:m>2或m<-2
则m的取值范围是:{m|m>2或m<-2},
故答案为:{m|m>2或m<-2}.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
11.下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A. | y=($\frac{1}{2}$)x | B. | y=$\frac{1}{x-1}$ | C. | y=x+sinx | D. | y=-x3-x |
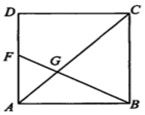 如图,在正方形 ABCD中,F是 AD 的中点,BF与 AC交于点 G,则△BGC 与四边形 CGFD的面积之比是4:5.
如图,在正方形 ABCD中,F是 AD 的中点,BF与 AC交于点 G,则△BGC 与四边形 CGFD的面积之比是4:5.