题目内容
18.设$\frac{1}{2}$<($\frac{1}{2}$)b<($\frac{1}{2}$)a<1,那么( )| A. | 1<aa<ab | B. | aa<ab<1 | C. | ab<aa<1 | D. | 1ab<aa |
分析 根据指数函数的单调性求出a,b的范围,从而求出答案.
解答 解:∵f(x)=${(\frac{1}{2})}^{x}$是减函数,
∴1>b>a>0,
∴ab<aa<1,
故选:C.
点评 本题考查了指数函数的性质,考查函数的单调性问题,是一道基础题.

练习册系列答案
相关题目
8.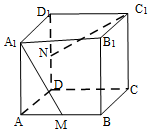 已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )
已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )
 已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )
已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
6.已知数列{an},它的前n项和为Sn,若an=$\frac{1}{(2n+1)(2n-1)}$,则Sn=( )
| A. | $\frac{2}{2n+1}$ | B. | $\frac{2n}{2n+1}$ | C. | $\frac{n}{2n+1}$ | D. | $\frac{1}{2n+1}$ |
10.若函数f(x)=$\left\{\begin{array}{l}{(a-5)x-2,x≥2}\\{{x}^{2}-2(a+1)x+3a,x<2}\end{array}\right.$ 对任意x1,x2∈R(x1≠x2),都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则实数a的取值范围为( )
| A. | (-∞,1] | B. | (1,5) | C. | [1,5) | D. | [1,4] |
7.下列说法中,正确的是( )
| A. | 数列{$\frac{n+1}{n}$} 的第k项为1+$\frac{1}{k}$ | |
| B. | 数列0,2,4,6,8…可记为{2n} | |
| C. | 数列1,0,-1与数列-1,0,1是相同的数列 | |
| D. | 数列1,3,5,7可表示为{1,3,5,7} |
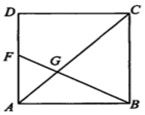 如图,在正方形 ABCD中,F是 AD 的中点,BF与 AC交于点 G,则△BGC 与四边形 CGFD的面积之比是4:5.
如图,在正方形 ABCD中,F是 AD 的中点,BF与 AC交于点 G,则△BGC 与四边形 CGFD的面积之比是4:5.