Question

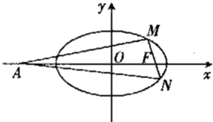如图所示，已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

6

3

，F为椭圆在x轴正半轴上的焦点，M、N两点在椭圆C上，且

MF

=λ

FN

（λ＞0），定点A（-4，0），当λ=1时，有

AM

•

AN

=

106

3

．
（Ⅰ）求椭圆C的方程．
（Ⅱ）当M、N两点在椭圆C上运动时，试判断

AM

•

AN

•tan∠MAN是否有最大值，若存在，求出最大值，并求出这时M、N两点所在直线方程，若不存在，请说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：计算题,平面向量及应用,圆锥曲线的定义、性质与方程

分析：（Ⅰ）求出M，N的坐标，由向量的数量积的坐标公式，得到c的方程，解出即可得到椭圆方程；
（Ⅱ）运用向量的数量积的定义，设直线MN的方程为y=k（x-2），k≠0，联立直线方程和椭圆方程，消去y，运用韦达定理，配方得到，结合二次函数的最值，即可得到．

解答： 解：（Ⅰ）当λ=1时，不妨设M(c，

b2

a

)，N(c，-

b2

a

)，
∴

AM

•

AN

=(c+4)2-

b4

a2

，
又a2=

3

2

c2，b2=

c2

2

，
∴

5

6

c2+8c+16=

106

3

．
∵c＞0，∴c=2，椭圆C的方程为

x2

6

+

y2

2

=1；
（Ⅱ）

AM

•

AN

×tan∠MAN=2S_△AMN=|AF||y_M-y_N|，
设直线MN的方程为y=k（x-2），k≠0，
联立

y=k(x-2) x2 6 + y2 2 =1

，
得（1+3k²）y²+4ky-2k²=0，
y_M+y_N=-

4k

1+3k2

，y_My_N=

-2k2

1+3k2

，
∴|yM-yN|=

24k4+24k2

1+3k2

．
记t=

24k4+24k2

1+3k2

，S=1+3k²，
则t=

24 • ( S-1 3 )2+( S-1 3 )

S

=

2 6

3

•

1+ 1 S - 2 S2

，
∴当t≤

3

，当S=4，即k=±1时取等号．
并且当k=0时，

AM

•

AN

×tan∠MAN=0，
当k不存在时|yM-yN|=

2 6

3

＜

3

．
综上

AM

•

AN

×tan∠MAN有最大值，最大值为6

3

．
此时，直线MN的方程为x-y-2=0或x+y-2=0．

点评：本题考查椭圆方程和性质，考查平面向量的数量积的定义和性质，以及联立直线方程和椭圆方程，消去未知数，运用韦达定理，考查运算能力，属于中档题和易错题．